题目内容
定义在(-1,1)上的函数f(x)是奇函数,且当x∈(0,1)时,f(x)=| 2x | 4x+1 |
(1)求f(x)在(-1,1)上的解析式;
(2)判断f(x)在(0,1)上的单调性,并给予证明;
(3)当实数λ为何值时,关于x的方程f(x)=λ在(-1,1)上有解?
分析:(1)定义在R上的奇函数f(x),可得f(0)=0,及x∈(-1,0)时f(x)的解析式,x=-1和1时,同时结合奇偶性和单调性求解.
(2)证明单调性可用定义或导数解决.
(3)利用(2)的结果得出函数在区间在(-1,1)上的取值范围,从而得出x的方程f(x)=λ在(-1,1)上有解的实数λ的范围即可.
(2)证明单调性可用定义或导数解决.
(3)利用(2)的结果得出函数在区间在(-1,1)上的取值范围,从而得出x的方程f(x)=λ在(-1,1)上有解的实数λ的范围即可.
解答:解:(1)当x∈(-1,0)时,-x∈(0,1).
∵f(x)是奇函数,∴f(x)=-f(-x)=-
=-
由f(0)=f(-0)=-f(0),
得f(0)=0.
∴在区间[-1,1]上,有f(x)=
(2)证明当x∈(0,1)时,f(x)=
,设0<x1<x2<1,
则f(x1)-f(x2)=
-
=
∵0<x1<x2<1,∴2x2-2x1>0,2x2+x1-1>0,∴f(x1)-f(x2)>0,即f(x1)>f(x2),
故f(x)在(0,1)上单调递减.
(3)由(2)得,函数f(x)在区间在(-1,1)上的取值范围是(
,
)∪(-
,
)∪{0}.
∴当实数λ∈(
,
)∪(-
,
)∪{0}时,关于x的方程f(x)=λ在(-1,1)上有解
∵f(x)是奇函数,∴f(x)=-f(-x)=-
| 2-x |
| 4-x+1 |
| 2x |
| 4x+1 |
由f(0)=f(-0)=-f(0),
得f(0)=0.
∴在区间[-1,1]上,有f(x)=
|
(2)证明当x∈(0,1)时,f(x)=
| 2x |
| 4x+1 |
则f(x1)-f(x2)=
| 2x1 |
| 4x1+1 |
| 2x2 |
| 4x2+1 |
| (2x2-2x1)(2x1+x2-1) |
| (4x1+1)(4x2+1) |
∵0<x1<x2<1,∴2x2-2x1>0,2x2+x1-1>0,∴f(x1)-f(x2)>0,即f(x1)>f(x2),
故f(x)在(0,1)上单调递减.
(3)由(2)得,函数f(x)在区间在(-1,1)上的取值范围是(
| 2 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 5 |
∴当实数λ∈(
| 2 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 5 |
点评:本题考查奇偶性、函数单调性的判断与证明的综合应用,及函数与方程的综合运用,综合性较强.

练习册系列答案
相关题目
 是定义在(-1,1)的奇函数,且f(
是定义在(-1,1)的奇函数,且f( )=
)= .
.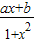 是定义在(-1,1)的奇函数,且f(
是定义在(-1,1)的奇函数,且f( )=
)= .
.