题目内容
在△ABC中,设内角A、B、C的对边分别为a、b、c,cos(C+| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
(1)求角C的大小;
(2)若c=2
| 3 |
分析:(1)首先利用余弦的和差公式化简cos(C+
)+cos(C-
)=
,再根据角的范围求出C的度数;
(2)利用正弦定理sinA=2sinB得出a=2b,再利用余弦定理求出a、b的值,然后根据S△ABC=
absinC=2
.
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
(2)利用正弦定理sinA=2sinB得出a=2b,再利用余弦定理求出a、b的值,然后根据S△ABC=
| 1 |
| 2 |
| 3 |
解答:解:(1)∵cos(C+
)+cos(C-
)=
,2cosCcos
=
,
∴cosC=
,
∵在△ABC中,0<C<π,
∴C=
.
(2)∵sinA=2sinB
∴a=2b
∵c2=a2+b2-2abcosC
∴(2
)2=4b2+b2-2•2bb•
=3b2
∴b=2,∴a=4,∴S△ABC=
absinC=2
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
| π |
| 4 |
| ||
| 2 |
∴cosC=
| 1 |
| 2 |
∵在△ABC中,0<C<π,
∴C=
| π |
| 3 |
(2)∵sinA=2sinB
∴a=2b
∵c2=a2+b2-2abcosC
∴(2
| 3 |
| 1 |
| 2 |
∴b=2,∴a=4,∴S△ABC=
| 1 |
| 2 |
| 3 |
点评:本题主要考查了同角三角函数基本关系的应用、正余弦定理的运用,(1)问中注意角C的范围.属于基础题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
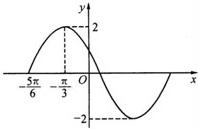 已知函数f(x)=2sin(ωx+φ)(ω>0,0<φ<2π)在一个周期内的图象如图所示.
已知函数f(x)=2sin(ωx+φ)(ω>0,0<φ<2π)在一个周期内的图象如图所示.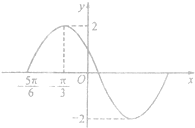 已知函数f(x)=2sin(ωx+φ)(ω>0,0<φ<2π)在一个周期内的图象如图所示.
已知函数f(x)=2sin(ωx+φ)(ω>0,0<φ<2π)在一个周期内的图象如图所示.