题目内容
函数f（x）=x3+ax2+bx+a2在x=1时有极值为10，则a+b的值为________．
-7
分析：首先对f（x）求导，然后由题设在x=1时有极值10可得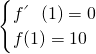
，解方程得出a，b的值，最后求它们的即可．
解答：对函数f（x）求导得 f′（x）=3x2+2ax+b，
又∵在x=1时f（x）有极值10，
∴
，
解得
或 
，
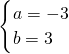验证知，当a=-3，b=3时，在x=1无极值，
故 a+b的值-7．
故答案为：-7
点评：掌握函数极值存在的条件，考查利用函数的极值存在的条件求参数的能力．
分析：首先对f（x）求导，然后由题设在x=1时有极值10可得
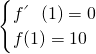，解方程得出a，b的值，最后求它们的即可．解答：对函数f（x）求导得 f′（x）=3x2+2ax+b，
又∵在x=1时f（x）有极值10，
∴
，解得
或 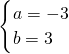，验证知，当a=-3，b=3时，在x=1无极值，
故 a+b的值-7．
故答案为：-7
点评：掌握函数极值存在的条件，考查利用函数的极值存在的条件求参数的能力．
练习册系列答案
相关题目