题目内容
设命题 函数
函数 在定义域上为减函数;命题
在定义域上为减函数;命题
 ,当
,当 时,
时, ,以下说法正确的是( )
,以下说法正确的是( )
A.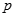  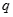 为真 为真 | B.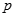  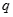 为真 为真 | C.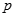 真 真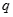 假 假 | D.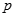 , ,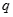 均假 均假 |
D
解析试题分析:函数 在(-∞,0),(0,+∞)上是减函数,在定义域{x|x≠0}上不具有单调性,∴命题p是假命题;由a+b=1得b=1-a,带入
在(-∞,0),(0,+∞)上是减函数,在定义域{x|x≠0}上不具有单调性,∴命题p是假命题;由a+b=1得b=1-a,带入 并整理得:3a2-3a+1=0,∴△=9-12<0,∴该方程无解,即不存在a,b∈(0,+∞),当a+b=1时,
并整理得:3a2-3a+1=0,∴△=9-12<0,∴该方程无解,即不存在a,b∈(0,+∞),当a+b=1时, ,∴命题q是假命题;∴p,q均价,∴p∨q为假,p∧q为假;故选D.
,∴命题q是假命题;∴p,q均价,∴p∨q为假,p∧q为假;故选D.
考点:复合命题的真假.

练习册系列答案
相关题目
下列有关命题的说法正确的是( )
A.命题“ ,均有 ,均有 ”的否定是:“ ”的否定是:“ ,使得 ,使得 ” ” |
B.“ ”是“ ”是“ ”成立的充分不必要条件 ”成立的充分不必要条件 |
C.线性回归方程 对应的直线一定经过其样本数据点 对应的直线一定经过其样本数据点 中的一个点 中的一个点 |
D.若“ ”为真命题,则“ ”为真命题,则“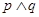 ”也为真命题 ”也为真命题 |
已知命题 :
: ,
, ,则( )
,则( )
A.¬ : : , , |
B.¬ : : , , |
C.¬ : : , , |
D.¬ : : , , |
设 ,则“
,则“ ”是“
”是“ ”的( )
”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
如果函数 在区间
在区间 上单调递减,那么实数
上单调递减,那么实数 的取值范围是 ( )
的取值范围是 ( )
A. | B. | C. | D. |
函数 的反函数是( )
的反函数是( )
A. | B. |
C. | D. |
 ,集合
,集合 ,集合
,集合 .
. ; (Ⅱ)
; (Ⅱ) .
. ,则
,则 互为相反数”的逆命题;
互为相反数”的逆命题; ,则
,则 有实根”的逆否命题.
有实根”的逆否命题. ,则
,则 = .
= .