Question

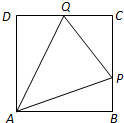某生态园要对一块边长为1km的正方形区域ABCD进行规划，设计了如图所示的三条参观路线．具体设计方案如下：从A出发到达BC边上的P点，然后从P点出发到达CD边上的Q点，再直接回到A点，其中要求∠PAQ=45°，设∠PAB=θ，tanθ=t．
（1）用t表示路径AQ的长度；
（2）将△APQ的面积表示为t的函数f（t），并注明其定义域；
（3）欲使△APQ的面积最小，应如何确定点P的位置．

Answer 1

分析：（1）利用已知条件，结合直角三角形，直接用t表示出DQ的长度，利用勾股定理求AQ的长度．
（2）利用S=S_{正方形ABCD}-S_△ABP-S_△ADQ，求出函数f（t），并求函数的定义域．
（3）利用（2）求出的面积S，利用基本不等式求出面积的最小值，并确定P的位置．

解答：解：（1）因为tanθ=t，则0≤t≤1，又tanθ=

BP

AB

=BP=t，所以BP=t，CP=1-t．
因为∠PAQ=45°，∠PAB=θ，所以∠DAQ=90°-45°-θ=45°-θ，
因为tan∠DAQ=DQ，所以DQ=tan∠DAQ=tan（45°-θ）=

1-t

1+t

，
所以AQ=

AD2+DQ2

=

1+( 1-t 1+t )2

=

2(1+t2)

1+t

．
（2）△APQ的面积表示为t的函数f（t）=S_{正方形ABCD}-S_△ABP-S_△ADQ，
因为CQ=1-DQ，所以CQ=1-

1-t

1+t

=

2t

1+t

所以f（t）=S_{正方形ABCD}-S_△ABP-S_△ADQ=1-(

1

2

?

1-t

1+t

+

1

2

(1-t)?

2t

1+t

+

1

2

?t)=1+

1

2

?

t2-2t-1

1+t

，（0≤t≤1）．
（3）因为f（t）=1+

1

2

?

t2-2t-1

1+t

=1+

1

2

?

(t+1)2-4(t+1)+2

1+t

=1+

1

2

[(t+1)+

2

1+t

-4]，
所以由基本不等式得f（t）=1+

1

2

[(t+1)+

2

1+t

-4]≥1+

1

2

[2

(t+1)? 2 1+t

-4]=1+

1

2

(2

2

-4)=1+

2

-2=

2

-1，
当且仅当t+1=

2

1+t

，即（t+1）²=2，t=

2

-1时取等号．
此时P满足BP=

2

-1．

点评：本题主要考查与函数有关的应用题，综合考查的勾股定理，三角函数的定义和三角关系，以及基本不等式基本应用，考查学生的运算能力，综合性较强，难度较大．