题目内容
已知函数
在R上有意义，则实数a的取值范围是________．
（0，1）∪（1，4）
分析：根据对数函数在R上恒有意义，真数恒大于0，可得关于a的不等式，结合底数a＞0且a≠1，可得实数a的取值范围
解答：∵函数在R上有意义
∴x2-ax+4＞0恒成立
即△=a2-16＜0
解得-4＜a＜4
又∵a＞0且a≠1
∴实数a的取值范围是（0，1）∪（1，4）
故答案为：（0，1）∪（1，4）
点评：本题考查的知识点是对数函数的图象与性质的综合应用，其中分析出真数恒为正，将问题转化为恒成立问题是解答的关键．但易忽略底数对a的限制．
分析：根据对数函数在R上恒有意义，真数恒大于0，可得关于a的不等式，结合底数a＞0且a≠1，可得实数a的取值范围
解答：∵函数
在R上有意义∴x2-ax+4＞0恒成立
即△=a2-16＜0
解得-4＜a＜4
又∵a＞0且a≠1
∴实数a的取值范围是（0，1）∪（1，4）
故答案为：（0，1）∪（1，4）
点评：本题考查的知识点是对数函数的图象与性质的综合应用，其中分析出真数恒为正，将问题转化为恒成立问题是解答的关键．但易忽略底数对a的限制．
练习册系列答案
阅读快车系列答案
相关题目
在R上存在极值；
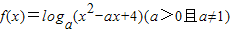，都有
；
为真，
为假，试求实数a的取值范围。
，函数
有意义；
在R上有意义，则实数a的取值范围是 ．
在R上有意义，则实数a的取值范围是 ．