题目内容
已知函数 .求:
.求:
(Ⅰ)函数f(x)的最小正周期;
(Ⅱ)函数f(x)的单调增区间.
解: =
= .
.
(Ⅰ)函数f(x)的最小正周期是 ;
;
(Ⅱ)当2kπ-π≤2x≤2kπ,即 (k∈Z)时,
(k∈Z)时,
函数 是增函数,
是增函数,
故函数f(x)的单调递增区间是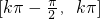 (k∈Z).
(k∈Z).
分析:(Ⅰ)利用倍角公式,把函数化为一个角的一个三角函数的形式,然后求函数f(x)的最小正周期;
(Ⅱ)利用(Ⅰ)以及余弦函数的单调性,求函数f(x)的单调增区间.
点评:本题考查三角函数的周期性及其求法,二倍角的余弦,余弦函数的单调性,考查学生分析问题解决问题的能力,是基础题.
 =
= .
.(Ⅰ)函数f(x)的最小正周期是
 ;
;(Ⅱ)当2kπ-π≤2x≤2kπ,即
 (k∈Z)时,
(k∈Z)时,函数
 是增函数,
是增函数,故函数f(x)的单调递增区间是
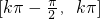 (k∈Z).
(k∈Z).分析:(Ⅰ)利用倍角公式,把函数化为一个角的一个三角函数的形式,然后求函数f(x)的最小正周期;
(Ⅱ)利用(Ⅰ)以及余弦函数的单调性,求函数f(x)的单调增区间.
点评:本题考查三角函数的周期性及其求法,二倍角的余弦,余弦函数的单调性,考查学生分析问题解决问题的能力,是基础题.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
 ,求:
,求:
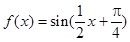 ,求函数在区间
,求函数在区间 上的单调增区间;
上的单调增区间; .
. ,
,
 的最大值和最小正周期;
的最大值和最小正周期; 的内角
的内角 的对边分别
的对边分别 且
且 ,
, ,若
,若 求
求 的值.
的值. .
. ,试求函数在此区间上的最大值与最小值.
,试求函数在此区间上的最大值与最小值. ,求:
,求: