题目内容
(理)以椭圆的右焦点F2为圆心作一个圆,使此圆过椭圆中心O并交椭圆于点M、N,若过椭圆左焦点F1的直线MF1是圆F2的切线,则椭圆的右准线与圆F2A.相交 B.相离
C.相切 D.位置关系随离心率改变
答案：(理)A 由已知得|MF2|=c,|MF1|=2a-c,
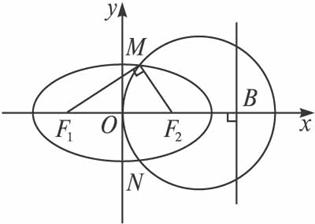
又MF1⊥MF2,∴(2a-c)2+c2=4c2.
解得4a2-4ac-2c2=0,a=
c.
|F2B|=
,∴与准线相交.∴选A.
练习册系列答案
相关题目
题目内容
(理)以椭圆的右焦点F2为圆心作一个圆,使此圆过椭圆中心O并交椭圆于点M、N,若过椭圆左焦点F1的直线MF1是圆F2的切线,则椭圆的右准线与圆F2A.相交 B.相离
C.相切 D.位置关系随离心率改变
答案：(理)A 由已知得|MF2|=c,|MF1|=2a-c,
又MF1⊥MF2,∴(2a-c)2+c2=4c2.
解得4a2-4ac-2c2=0,a=c.
|F2B|=,∴与准线相交.∴选A.
（a>b>0）上，以M为圆心的圆与x轴相切于椭圆的右焦点F。
的准线与
轴交于
，焦点为
；以
为焦点，离心率
的椭圆
与抛物线
在
.
时，求椭圆的方程及其右准线的方程；
经过椭圆
，如果
为直径作圆，试判断点P与圆的位置关系，并说明理由；
，使得△
的边长是连续的自然数，若存在，求出这样的实数
的右焦点F为圆心，a为半径的圆与椭圆的右准线交于不同的两点，则该椭圆的离心率的取值范围是 （ ）
B．
C．
D．
的右焦点
为圆心，
为半径的圆与椭圆的右准线交于不同的两点，则该椭圆的离心率的取值范围是
B、
C、
D、