题目内容
13.向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,|$\overrightarrow{c}$|=3,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°,则|$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$|最小值为( )| A. | 3+$\sqrt{3}$ | B. | 3-$\sqrt{3}$ | C. | 3+$\sqrt{7}$ | D. | 3-$\sqrt{7}$ |
分析 通过作向量$\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$即可看出当$\overrightarrow{c}$和$\overrightarrow{a}+\overrightarrow{b}$方向相反时,$|\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}|$最小,根据条件可求|$\overrightarrow{a}+\overrightarrow{b}$|,从而可求出$|\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}|$的最小值.
解答 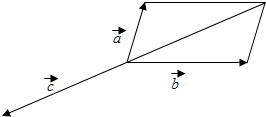 解:如图,将向量$\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$移到同一起点,当$\overrightarrow{c}$和$\overrightarrow{a}+\overrightarrow{b}$反向时|$\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}$|最小;
解:如图,将向量$\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$移到同一起点,当$\overrightarrow{c}$和$\overrightarrow{a}+\overrightarrow{b}$反向时|$\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}$|最小;
根据条件:$|\overrightarrow{a}+\overrightarrow{b}|=\sqrt{(\overrightarrow{a}+\overrightarrow{b})^{2}}=\sqrt{1+4+2}=\sqrt{7}$;
又$|\overrightarrow{c}|=3$;
∴$|\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}|$的最小值为3-$\sqrt{7}$.
故选D.
点评 考查向量加法的平行四边形法则,三角形的两边之差小于第三边,以及向量长度的求法|$\overrightarrow{a}+\overrightarrow{b}$|=$\sqrt{(\overrightarrow{a}+\overrightarrow{b})^{2}}$,数量积的运算.

| A. | 因为∠A和∠B是两条平行直线被第三条直线所截得的同旁内角,所以∠A+∠B=180° | |
| B. | 我国地质学家李四光发现中国松辽地区和中亚细亚的地质结构类似,而中亚细亚有丰富的石油,由此,他推断松辽平原也蕴藏着丰富的石油 | |
| C. | 由6=3+3,8=3+5,10=3+7,12=5+7,14=7+7,…,得出结论:一个偶数(大于4)可以写成两个素数的和 | |
| D. | 在数列{an}中,a1=1,an=$\frac{1}{2}$(an-1+$\frac{1}{{a}_{n-1}}$)(n≥2),通过计算a2,a3,a4,a5的值归纳出{an}的通项公式 |
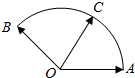 给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°.点C在以OA,OB为半径的圆弧上,∠AOC=30°如图所示,若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x=$\frac{2\sqrt{3}}{3}$;y=$\frac{\sqrt{3}}{3}$.
给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°.点C在以OA,OB为半径的圆弧上,∠AOC=30°如图所示,若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x=$\frac{2\sqrt{3}}{3}$;y=$\frac{\sqrt{3}}{3}$. 设△ABC的内角A、B、C所对的边分别为a、b、c,$\frac{5(sinA-sinC)}{sin(A+C)}=\frac{5sinB-8sinC}{sinA+sinC}$,点P为△ABC内任意一点,点P到三边的距离之和为d.
设△ABC的内角A、B、C所对的边分别为a、b、c,$\frac{5(sinA-sinC)}{sin(A+C)}=\frac{5sinB-8sinC}{sinA+sinC}$,点P为△ABC内任意一点,点P到三边的距离之和为d.