题目内容
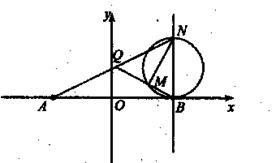
已知定点A（－2，0），动点B是圆F：
（F为圆心）上一点，线段AB的垂直平分线交BF于P.
（1）求动点P的轨迹E的方程；
（2）直线
交于M，N两点，试问在曲线E位于第二象限部分上
是否存在一点C，使
共线（O为坐标原点）？若存在，求出点C的坐标；若不存在，请说明理由.
解：（1）由题意
∴
因此点P的轨迹是以A，F为焦点的椭圆.……………………4分
设所求椭圆的方程为
∴
∴
∴点P的轨迹方程为
…………………………6分
（2）假设存在满足题意的点
由
……………………8分
……………………10分 又
又
所以存在满足题意的点C（
）……………………14分
练习册系列答案
相关题目
（本题满分14分）
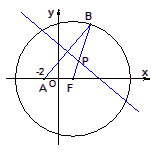已知定点A（－2，0），动点B是圆
（F为圆心）上一点，线段AB的垂直平分线交BF于P．
（1）求动点P的轨迹方程；
|
（O为原点）．若存在，求直线l的方程；若不存在，请说明理由． 
已知定点A（－2，0），动点B是圆
（F为圆心）上一点，线段AB的垂直平分线交BF于P．
（O为原点）．若存在，求直线l的方程；若不存在，请说明理由．
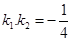，其中k1、k2分别表示直线AP、BP的斜率．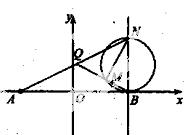
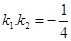，其中k1、k2分别表示直线AP、BP的斜率．