题目内容
20.设函数f(x)=|x-1|+|x-a|.(1)若a=-1,解不等式f(x)≥3
(2)如果?x∈R,f(x)≥2,求a的取值范围.
分析 (1)若a=-1,由绝对值的意义求得不等式f(x)≥3的解集.
(2)由条件利用绝对值的意义求得函数f(x)的最小值为|a-1|,可得|a-1|=2,由此求得a的值.
解答 解:(1)若a=-1,函数f(x)=|x-1|+|x-a|=|x-1|+|x+1|,表示数轴上的x对应点到1、-1对应点的距离之和,
而-1.2和 1.5 对应点到1、-1对应点的距离之和正好等于3,
故不等式f(x)≥3的解集为{x|≤-1.5,或 x≥1.5}.
(2)由于?x∈R,f(x)≥2,故函数f(x)的最小值为2.
函数f(x)=|x-1|+|x-a|表示数轴上的x对应点到1、a对应点的距离之和,它的最小值为|a-1|,
即|a-1|=2,求得a=3 或a=-1.
点评 本题主要考查绝对值的意义,函数的恒成立问题,属于中档题.

练习册系列答案
相关题目
10.数列{an}中,a1=1,a1•a2…an=n2,则a3-a5=( )
| A. | $\frac{1}{16}$ | B. | -$\frac{1}{16}$ | C. | $\frac{11}{16}$ | D. | -$\frac{11}{16}$ |
11.曲线y=x2-2x与直线x=-1,x=1以及x轴所围图形的面积为( )
| A. | 2 | B. | $\frac{8}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |
8.如图所示,在“推理与证明”的知识结构图中,如果要加入“综合法”,则应该放在( )
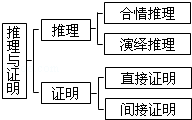

| A. | “合情推理”的下位 | B. | “直接证明”的下位 | ||
| C. | “演绎推理”的下位 | D. | “间接证明”的下位 |
5.将甲、乙、丙三位新同学分到2个不同的班级,每班至少1人,则甲、乙被分到同一个班的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
9.已知等比数列{an}的前项和为Sn=2×(-1)n+a,n∈N*,则实数a的值是( )
| A. | -3 | B. | -2 | C. | -1 | D. | 0 |
10.已知函数f(x)=sin(ωx+$\frac{π}{6}$),其中ω>0,若f($\frac{π}{6}$)=f($\frac{π}{3}$),且f(x)在区间($\frac{π}{6}$,$\frac{π}{3}$)上有最小值、无最大值,则ω等于( )
| A. | $\frac{40}{3}$ | B. | $\frac{28}{3}$ | C. | $\frac{16}{3}$ | D. | $\frac{4}{3}$ |
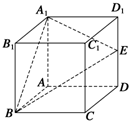 如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点.在棱C1D1上是否存在一点F,使B1F∥平面A1BE?证明你的结论.
如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点.在棱C1D1上是否存在一点F,使B1F∥平面A1BE?证明你的结论.