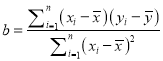题目内容
【题目】若函数![]() ,
, ![]() ,则对于不同的实数
,则对于不同的实数![]() ,函数
,函数![]() 的单调区间个数不可能是( )
的单调区间个数不可能是( )
A. 1个 B. 2个 C. 3个 D. 5个
【答案】B
【解析】 由题意,(1)当![]() 时,
时, ![]() 在
在![]() 上为增函数,只有一个单调区间,
上为增函数,只有一个单调区间,
当![]() 时,因为
时,因为![]() ,
,
所以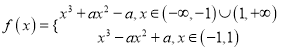
所以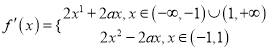
(2)当![]() 时,因为
时,因为![]() ,
,
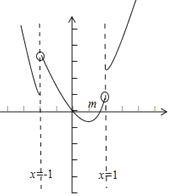
所以导数的图象如图所示,其中![]() 为图象与
为图象与![]() 轴的交点横坐标,
轴的交点横坐标,
所以![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() ,
,
所以![]() 在
在![]() 时,单调递增;
时,单调递增; ![]() 时,单调递减;
时,单调递减; ![]() 时,单调递增,所以函数
时,单调递增,所以函数![]() 有三个单调区间.
有三个单调区间.
(3)当![]() 时,
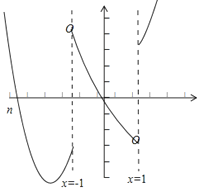
时, ![]() ,所以导数的图象如图所示(其中
,所以导数的图象如图所示(其中![]() 为
为![]() 时图象与
时图象与![]() 轴交点的横坐标)
轴交点的横坐标)
所以当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
所以![]() 在
在![]() 时,单调递增;
时,单调递增; ![]() 时,单调递减;
时,单调递减; ![]() 时,单调递增,
时,单调递增, ![]() 时,单调递减;
时,单调递减; ![]() 时,单调递增,共有5个单调区间,
时,单调递增,共有5个单调区间,
由此可得A、C、D不正确,故选B.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目