题目内容
已知数列{an}满足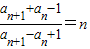 (n为正整数)且a2=6,则数列{an}的通项公式为an= .
(n为正整数)且a2=6,则数列{an}的通项公式为an= .
【答案】分析:由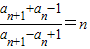 可得an+1+an-1=nan+1-nan+n,构造可得
可得an+1+an-1=nan+1-nan+n,构造可得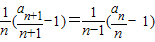 即
即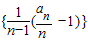 为常数列,从而可求
为常数列,从而可求
解答:解:由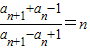 可得an+1+an-1=nan+1-nan+n
可得an+1+an-1=nan+1-nan+n
∴(1-n)an+1+(1+n)an=1+n
∴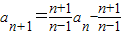 =
=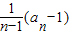 ×(n+1)
×(n+1)
∴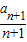 =
=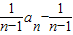 =
=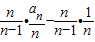
∴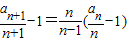
∴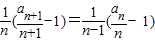
∴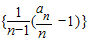 为常数列
为常数列
而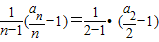 =2
=2
an=[2(n-1)+1]n=2n2-n
当n=1时,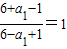 可得a1=1适合上式
可得a1=1适合上式
故答案为:2n2-n
点评:本题目主要考查了利用数列的递推公式求解数列的通项公式,解题得关键是利用递推公式构造特殊数列.
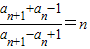 可得an+1+an-1=nan+1-nan+n,构造可得
可得an+1+an-1=nan+1-nan+n,构造可得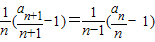 即
即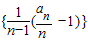 为常数列,从而可求
为常数列,从而可求解答:解:由
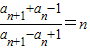 可得an+1+an-1=nan+1-nan+n
可得an+1+an-1=nan+1-nan+n∴(1-n)an+1+(1+n)an=1+n
∴
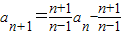 =
=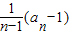 ×(n+1)
×(n+1)∴
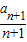 =
=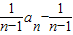 =
=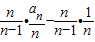
∴
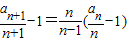
∴
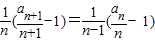
∴
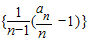 为常数列
为常数列而
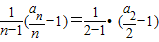 =2
=2an=[2(n-1)+1]n=2n2-n
当n=1时,
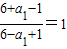 可得a1=1适合上式
可得a1=1适合上式故答案为:2n2-n
点评:本题目主要考查了利用数列的递推公式求解数列的通项公式,解题得关键是利用递推公式构造特殊数列.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目