题目内容
已知函数 和
和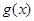 的图像关于原点对称,且
的图像关于原点对称,且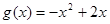 .
.
(1)求函数 的解析式;
的解析式;
(2)解不等式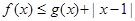 ;
;
(3)若函数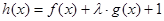 在区间
在区间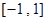 上是增函数,求实数
上是增函数,求实数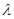 的取值范围.
的取值范围.
(1)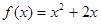 ;(2) 解集为
;(2) 解集为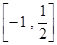 ;(3)
;(3) 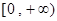 .
.
解析试题分析:(1)两个函数的图象关于某点或某条直线对称,一般设待求解析式的函数图象上任一点的坐标为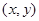 ,求出这点的对称点的坐标
,求出这点的对称点的坐标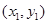 ,当然这里
,当然这里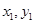 是用
是用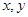 表示的式子,然后把点
表示的式子,然后把点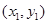 代入已知解析式,就能求出结论;(2)这是含有绝对值的不等式,解题时,一般按照绝对值的定义分类讨论以去掉绝对值符号,便于解题;(3)
代入已知解析式,就能求出结论;(2)这是含有绝对值的不等式,解题时,一般按照绝对值的定义分类讨论以去掉绝对值符号,便于解题;(3) 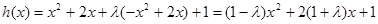 ,这是含参数的二次函数,解题时,首先对二次项系数
,这是含参数的二次函数,解题时,首先对二次项系数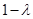 分类,即分二次项系数
分类,即分二次项系数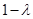 为0,不为0,其中
为0,不为0,其中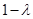 不为0还要分为是正数,还是负数进行讨论,在二次项系数
不为0还要分为是正数,还是负数进行讨论,在二次项系数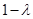 不为0时,只要讨论其对称轴与给定区间的关系就能求得结论.
不为0时,只要讨论其对称轴与给定区间的关系就能求得结论.
试题解析:(1)设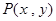 是函数
是函数 图像上任一点,则
图像上任一点,则 关于原点对称的点
关于原点对称的点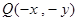 在函数
在函数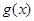 的图像上, (1分)
的图像上, (1分)
所以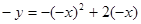 ,故
,故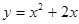 . (2分)
. (2分)
所以,函数 的解析式是
的解析式是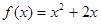 . (1分)
. (1分)
(2)由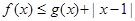 ,得
,得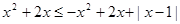 , (1分)
, (1分)
即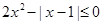 . (1分)
. (1分)
当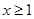 时,有
时,有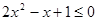 ,△
,△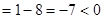 ,不等式无解; (1分)
,不等式无解; (1分)
当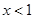 时,有
时,有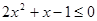 ,
,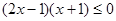 ,解得
,解得 . (2分)
. (2分)
综上,不等式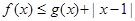 的解集为
的解集为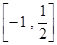 . (1分)
. (1分)
(3)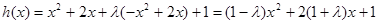 . (1分)
. (1分)
①当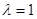 时,
时,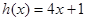 在区间
在区间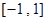 上是增函数,符合题意. (1分)
上是增函数,符合题意. (1分)
②当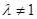 时,函数
时,函数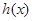 图像的对称轴是直线
图像的对称轴是直线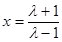 . (1分)
. (1分)
因为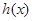 在区间
在区间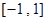 上是增函数,所以,
上是增函数,所以,
1)当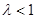 时,
时,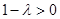 ,函数
,函数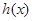 图像开口向上,故
图像开口向上,故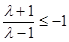 ,
,
解得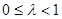 ; (1分)
; (1分)
2)当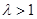 时,
时,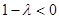 ,函数
,函数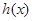 图像开口向下,故
图像开口向下,故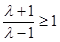 ,解得
,解得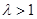 . (1分)
. (1分)
综上,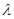 的取值范围是
的取值范围是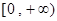 . (1分)
. (1分)
考点:(1)函数图象的对称问题;(2)含绝对值的不等式;(3)函数的单调性.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
 上的函数
上的函数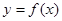 是偶函数,且
是偶函数,且 时,
时,  。
。 时,求
时,求 解析式;
解析式; ,求
,求 取值的集合;
取值的集合; ,函数的值域为
,函数的值域为 ,求
,求 满足的条件
满足的条件  上的函数
上的函数 同时满足以下条件:
同时满足以下条件: 在(0,1)上是减函数,在(1,+∞)上是增函数;
在(0,1)上是减函数,在(1,+∞)上是增函数; 是偶函数;
是偶函数; y=x+2垂直.
y=x+2垂直. =
= ,若存在实数x∈[1,e],使
,若存在实数x∈[1,e],使 <
< .
. 为偶函数,求
为偶函数,求 的值;
的值; ,求函数
,求函数 时,若对任意的
时,若对任意的 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 .
. ,试判断
,试判断 在定义域内的单调性;
在定义域内的单调性; 时,若
时,若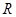 上有
上有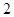 个零点,求
个零点,求 的取值范围.
的取值范围. R).
R). )上是增函数,求实数a的取值范围;
)上是增函数,求实数a的取值范围; ,且f(x0)=3,求x0的值;
,且f(x0)=3,求x0的值; ,且在R上是减函数,求实数a的取值范围。
,且在R上是减函数,求实数a的取值范围。 满足:对任意
满足:对任意 ,都有
,都有 成立,且
成立,且 时,
时, .
. 的值,并证明:当
的值,并证明:当 时,
时, ;
; 在
在 上递减,求实数
上递减,求实数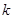 的取值范围.
的取值范围. ,x∈[1,3],
,x∈[1,3], 于任意的x∈[1,3],t∈[0,2]恒成立,求实数a的取值范围.
于任意的x∈[1,3],t∈[0,2]恒成立,求实数a的取值范围. 上的函数
上的函数 当
当 时,
时, ,且对任意的
,且对任意的 有
有 。
。 ,
, ,恒有
,恒有 ;
; ,求
,求 的取值范围。
的取值范围。