题目内容
(12分)已知函数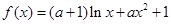 .
.
(Ⅰ)若函数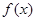 的最大值为1,求实数
的最大值为1,求实数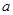 的值;
的值;
(Ⅱ)设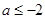 ,证明:对任意
,证明:对任意 ,
,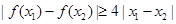 .
.
【答案】
(Ⅰ)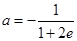 ;
;
(Ⅱ)证明略。
【解析】(Ⅰ) f(x)的定义域为(0,+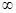 ),
),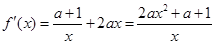 . … 1分
. … 1分
当a≥0时,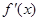 >0,故f(x)在(0,+
>0,故f(x)在(0,+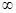 )单调增加;
… … 2分
)单调增加;
… … 2分
当a≤-1时,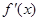 <0, 故f(x)在(0,+
<0, 故f(x)在(0,+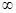 )单调减少;
… … 3分
)单调减少;
… … 3分
当-1<a<0时,令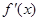 =0,解得x=
=0,解得x=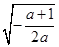 .当x∈(0,
.当x∈(0, 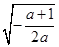 )时,
)时, 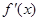 >0;
>0;
x∈(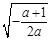 ,+
,+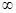 )时,
)时,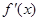 <0, 故f(x)在(0,
<0, 故f(x)在(0, 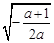 )单调增加,在(
)单调增加,在(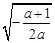 ,+
,+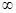 )单调减少.
… 5分
)单调减少.
… 5分
 当-1<a<0时
当-1<a<0时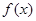 有最大值,
有最大值, 解得
解得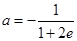 … 6分
… 6分
(Ⅱ)不妨假设x1≥x2.由于a≤-2,故f(x)在(0,+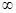 )单调减少.
)单调减少.
所以 等价于
等价于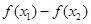 ≥4x1-4x2,
… … 8分
≥4x1-4x2,
… … 8分
即f(x2)+ 4x2≥f(x1)+ 4x1. 令g(x)=f(x)+4x,则
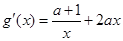 +4=
+4=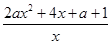 . … …
10分
. … …
10分
于是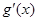 ≤
≤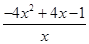 =
=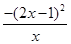 ≤0.
… … 11分
≤0.
… … 11分
从而g(x)在(0,+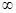 )单调减少,故g(x1) ≤g(x2),
)单调减少,故g(x1) ≤g(x2),
即f(x1)+ 4x1≤f(x2)+ 4x2,故对任意x1,x2∈(0,+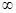 ) ,
) , .… 12分
.… 12分

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 ,
,
 与曲线
与曲线 在它们的交点(1,c)处具有公共切线,求
在它们的交点(1,c)处具有公共切线,求 ,
,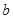 的值;
的值; ,
, 时,若函数
时,若函数 在区间[
在区间[ ,2]上的最大值为28,求
,2]上的最大值为28,求 ,
, 在
在 上的最大值为
上的最大值为 ,求实数
,求实数 的值;
的值; ,都有
,都有 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,对任意给定的正实数
,对任意给定的正实数 上是否存在两点
上是否存在两点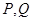 ,使得
,使得 是以
是以 (
( 轴上?请说明理由。
轴上?请说明理由。