题目内容
已知向量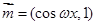 ,
,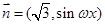 (
(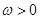 ),函数
),函数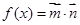 ,且
,且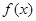 图象上一个最高点为
图象上一个最高点为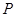
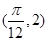 ,与
,与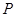 最近的一个最低点的坐标为
最近的一个最低点的坐标为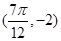 .
.
(1)求函数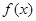 的解析式;
的解析式;
(2)设 为常数,判断方程
为常数,判断方程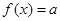 在区间
在区间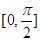 上的解的个数;
上的解的个数;
(3)在锐角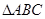 中,若
中,若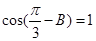 ,求
,求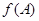 的取值范围.
的取值范围.
(1) (2)
(2) 或
或 时,方程一解;
时,方程一解; 时,方程两解;
时,方程两解; 或
或 时,方程无解.(3)
时,方程无解.(3)
解析试题分析:(1)求三角函数解析式,就是利用待定系数法,分别求出振幅、周期及初相. 由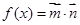 得
得
 又
又

 (2)方程
(2)方程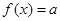 在区间
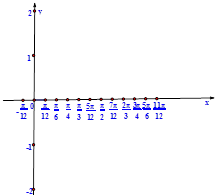
在区间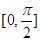 上的解的个数就是直线
上的解的个数就是直线 与曲线段
与曲线段 交点的个数.由图像知:
交点的个数.由图像知: 或
或 时,方程一解;
时,方程一解; 时,方程两解;
时,方程两解; 或
或 时,方程无解.(3)求
时,方程无解.(3)求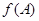 的取值范围,关键在于确定角A的取值范围. 因为
的取值范围,关键在于确定角A的取值范围. 因为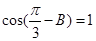 ,所以
,所以 ,
,

 ,
,

(1)

又

 4分
4分
(2)
 ,
, ,故有图像知
,故有图像知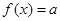 ,
,
所以 或
或 时,方程一解;
时,方程一解; 时,方程两解;
时,方程两解; 或
或 时,方程无解. 10分
时,方程无解. 10分
(3) ,
,

 ,
,
 16分
16分
考点:三角函数解析式,三角函数图像

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 上的函数y=f(x)的图象关于直线x=-
上的函数y=f(x)的图象关于直线x=- 对称,当x∈
对称,当x∈ 时,函数f(x)=Asin(ωx+φ)
时,函数f(x)=Asin(ωx+φ) 的图象如图所示.
的图象如图所示.
 的解.
的解. -
- )-2cos2
)-2cos2 .
. -A)+cos(π+A)=-
-A)+cos(π+A)=- .
. ,
, .
. ,求
,求 的最大值及相应的
的最大值及相应的 的取值集合;
的取值集合; 是
是 ,求
,求 的值和
的值和 0,
0, .
. 值; (2)求
值; (2)求 的值.
的值. 直线
直线 是
是 图像的任意两条对称轴,且
图像的任意两条对称轴,且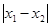 的最小值为
的最小值为 .
. 的单调增区间;
的单调增区间;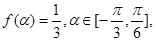 求
求 的值;
的值; 的方程
的方程 在
在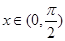 有实数解,求实数
有实数解,求实数 的取值.
的取值. ,函数
,函数 .
.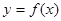 的周期和对称轴方程;
的周期和对称轴方程;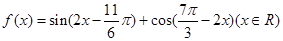 .
.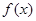 在一个周期内的图像
在一个周期内的图像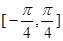 上的最大值和最小值.
上的最大值和最小值.