题目内容
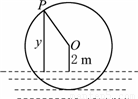
如图
为一半径是3m的水轮，水轮圆心O距离水面2m，已知水轮每分钟旋转4圈，水轮上的点P到水面的距离y（m）与时间t（s）满足函数关系y=Asin（ωt+?）+2（ω＞0，A＞0），则ω=
．
为一半径是3m的水轮，水轮圆心O距离水面2m，已知水轮每分钟旋转4圈，水轮上的点P到水面的距离y（m）与时间t（s）满足函数关系y=Asin（ωt+?）+2（ω＞0，A＞0），则ω=| 2π |
| 15 |
| 2π |
| 15 |
分析：先根据h的最大和最小值求得A和k，利用周期求得ω．
解答：解：∵水轮的半径为3，水轮圆心O距离水面2m，
A=3，k=2，
又水轮每分钟旋转4圈，故转一圈需要15秒，
∴T=15=
，
∴ω=
．
故答案为：
．
A=3，k=2，
又水轮每分钟旋转4圈，故转一圈需要15秒，
∴T=15=
| 2π |
| ω |
∴ω=
| 2π |
| 15 |
故答案为：
| 2π |
| 15 |
点评：题以实际问题为载体，考查三角函数模型的构建，考查学生分析解决问题的能力，解题的关键是构建三角函数式，利用待定系数法求得．
练习册系列答案
相关题目
为一半径是3m的水轮，水轮圆心O距离水面2m，已知水轮每分钟旋转4圈，水轮上的点P到水面的距离y（m）与时间t（s）满足函数关系y=Asin（ωt+?）+2（ω＞0，A＞0），则ω=________．
