Question

（2012•广州二模）如图，AB是圆O的直径，延长AB至C，使BC=2OB，CD是圆O的切线，切点为D，连接AD，BD，则面

AD

BD

的值为

2

．

Answer 1

分析：利用圆的切线构造直角三角形，求得tan∠DOB=2

2

，再利用∠DOB=2∠A，即可得到结论．

解答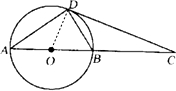：解：连接OD，则OD⊥CD，
∵BC=2OB，OB=OD，
∴OC=3OD，
∴DC=2

2

OD，
∴tan∠DOB=2

2

∵OA=OD，∴∠DOB=2∠A
∴tan2A=2

2

∴tan2A+

2

2

tanA-1=0
∴∴tan∠A=

2

2

（负值舍去）
∵AB是圆O的直径，∴∠ADB=90°
∴

AD

BD

=

1

tanA

==

2

故答案为：

2

点评：本题考查圆的切线的性质，考查三角函数，属于中档题．