题目内容
(难图象与性质)已知函数f(x)=2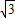 sin(2ωx+φ)(ω>0,φ∈(0,π))的图象中相邻两条对称轴间的距离为
sin(2ωx+φ)(ω>0,φ∈(0,π))的图象中相邻两条对称轴间的距离为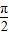 ,且点
,且点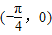 是它的一个对称中心.
是它的一个对称中心.(1)求f(x)的表达式;
(2)若f(ax)(a>0)在
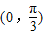 上是单调递减函数,求a的最大值.
上是单调递减函数,求a的最大值.
【答案】分析:(1)由题函数 的图象中相邻两条对称轴间的距离为
的图象中相邻两条对称轴间的距离为 可得周期是π,由此可求得ω=1,点
可得周期是π,由此可求得ω=1,点 是它的一个对称中心,可知
是它的一个对称中心,可知 在其图象上.代入可求得φ
在其图象上.代入可求得φ
(2)当x∈ 时,有ax∈(0,π)即可.
时,有ax∈(0,π)即可.
解答:解:(1)由题意得f(x)的最小正周期为π,∴ ,得ω=1.
,得ω=1.
∴ ,又
,又 是它的一个对称中心,.
是它的一个对称中心,.
∴ ,得
,得 ,
,
∴ .
.
(2)由(1)得f(ax)=2 cos2ax,∵
cos2ax,∵ ,
,
所以欲满足条件,必须 ,∴
,∴ .即a的最大值为
.即a的最大值为 .
.
点评:本题考点是由y=Asin(ωx+φ)的部分图象确定其解析式,将其图象特征转化成方程或不等式求出几个参数,得到解析式,此类题是在角函数知识综合运用的一个成熟题型.
 的图象中相邻两条对称轴间的距离为
的图象中相邻两条对称轴间的距离为 可得周期是π,由此可求得ω=1,点
可得周期是π,由此可求得ω=1,点 是它的一个对称中心,可知
是它的一个对称中心,可知 在其图象上.代入可求得φ
在其图象上.代入可求得φ(2)当x∈
 时,有ax∈(0,π)即可.
时,有ax∈(0,π)即可.解答:解:(1)由题意得f(x)的最小正周期为π,∴
 ,得ω=1.
,得ω=1.∴
 ,又
,又 是它的一个对称中心,.
是它的一个对称中心,.∴
 ,得
,得 ,
,∴
 .
.(2)由(1)得f(ax)=2
 cos2ax,∵
cos2ax,∵ ,
,所以欲满足条件,必须
 ,∴
,∴ .即a的最大值为
.即a的最大值为 .
.点评:本题考点是由y=Asin(ωx+φ)的部分图象确定其解析式,将其图象特征转化成方程或不等式求出几个参数,得到解析式,此类题是在角函数知识综合运用的一个成熟题型.

练习册系列答案
相关题目
 sin(2ωx+φ)(ω>0,φ∈(0,π))的图象中相邻两条对称轴间的距离为
sin(2ωx+φ)(ω>0,φ∈(0,π))的图象中相邻两条对称轴间的距离为 ,且点
,且点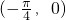 是它的一个对称中心.
是它的一个对称中心.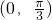 上是单调递减函数,求a的最大值.
上是单调递减函数,求a的最大值.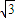 sin(2ωx+φ)(ω>0,φ∈(0,π))的图象中相邻两条对称轴间的距离为
sin(2ωx+φ)(ω>0,φ∈(0,π))的图象中相邻两条对称轴间的距离为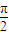 ,且点
,且点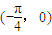 是它的一个对称中心.
是它的一个对称中心.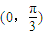 上是单调递减函数,求a的最大值.
上是单调递减函数,求a的最大值.