题目内容
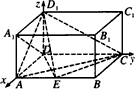
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动。
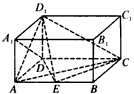
(1)证明:D1E⊥A1D;
(2)是否存在点E使得面D1DE⊥面D1EC?若存在,请求出此时点E到面ACD1的距离;若不存在,请说明理由;
(3)AE等于何值时,二面角D1-EC-D的大小为 ?
?
(2)是否存在点E使得面D1DE⊥面D1EC?若存在,请求出此时点E到面ACD1的距离;若不存在,请说明理由;
(3)AE等于何值时,二面角D1-EC-D的大小为
 ?
?| 解:如图,以D为坐标原点,直线DA,DC,DD1分别为x,y,z轴,建立空间直角坐标系, 设AE =x, 则 D(0,0,0),A(1,0,1),D(0,0,1),E(1,x,0),A(1,0,0),C(0,2,0) (1)因为 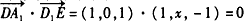 所以 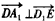 即D1E⊥A1D。 (2)设平面D1EC的一个法向量为n1=(a,b,c) 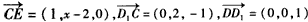 则 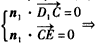 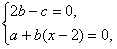 令b=1,则c=2,a=2-x,n1=(2-x,1,2), 再设平面D1DE的一个法向量为 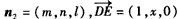 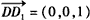 则 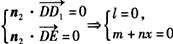 令n=1,则m=-x,n2=(-x,1,0) 由面D1DE⊥面D1EC  n1·n2=(2-x,1,2)·(-x,1,0)=0得x2-2x+1=0 n1·n2=(2-x,1,2)·(-x,1,0)=0得x2-2x+1=0故x=1 故E为AB的中点时,有面D1DE⊥面D1EC 由于此时点E为AB的中点,故E(1,1,0), 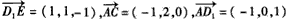 设平面ACD1的一个法向量n3=(x,y,z),则 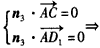 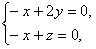 令x=2,则y=1,z=2,即n3=(2,1,2), 故点E到面ACD1的距离为 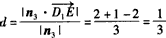 。 。(3)由上述解答过程可知面D1EC的法向量为n=(2-x,1,2) 由题意, 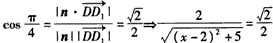 故 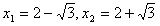 (不合题意,舍去) (不合题意,舍去)∴当 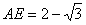 时,二面角D1-EC-D的大小为 时,二面角D1-EC-D的大小为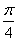 。 。 |
 |

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 如图在长方体ABCD-A1B1C1D1中,三棱锥A1-ABC的面是直角三角形的个数为:
如图在长方体ABCD-A1B1C1D1中,三棱锥A1-ABC的面是直角三角形的个数为: 如图,定义八个顶点都在某圆柱的底面圆周上的长方体叫做圆柱的内接长方体,圆柱也叫长方体的外接圆柱.设长方体ABCD-A1B1C1D1的长、宽、高分别为a,b,c(其中a>b>c),那么该长方体的外接圆柱侧面积的最大值等于( )
如图,定义八个顶点都在某圆柱的底面圆周上的长方体叫做圆柱的内接长方体,圆柱也叫长方体的外接圆柱.设长方体ABCD-A1B1C1D1的长、宽、高分别为a,b,c(其中a>b>c),那么该长方体的外接圆柱侧面积的最大值等于( )

 .
. 
 ,AA1 =
,AA1 = ,M为侧棱CC1上一点,AM⊥BA1.
,M为侧棱CC1上一点,AM⊥BA1.