题目内容
设S n是公差为d(d≠0)的无穷等差数列{a n}的前n项和,则下列命题错误的是
A.若d<0,则数列{S n}有最大项
B.若数列{S n}有最大项,则d<0
C.若数列{S n}是递增数列,则对任意的n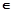 N*,均有S n>0
N*,均有S n>0
D.若对任意的n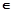 N*,均有S n>0,则数列{S n}是递增数列
N*,均有S n>0,则数列{S n}是递增数列
【答案】
C
【解析】
试题分析:A项中d<0,数列是递减数列,若 则存在
则存在 满足
满足
则 最大,若
最大,若 则
则 最大;B项中若
最大;B项中若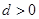 则
则 逐渐增大,无最大值;C项中当
逐渐增大,无最大值;C项中当 时
时 ,所以错误;D项中若数列是递减数列,则存在
,所以错误;D项中若数列是递减数列,则存在 满足当
满足当 时
时 恒成立,存在
恒成立,存在 满足
满足
考点:数列单调性与求和
点评:当数列是递增数列时 存在最小值,当数列是递减数列时
存在最小值,当数列是递减数列时 存在最大值
存在最大值

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 N*,均有S n>0
N*,均有S n>0