Question

（2006•朝阳区一模）已知椭圆

x2

a2

+

y2

b2

=1（a＞b＞0），中心在坐标原点O，一条准线的方程是x=1，过椭圆的左焦点F，且方向向量为

a

=（1，1）的直线l交椭圆于A、B两点，AB的中点为M．
（Ⅰ）求直线OM的斜率（用a、b表示）；
（Ⅱ）直线AB与OM的夹角为α，当tanα=2时，求椭圆的方程；
（Ⅲ）当A、B两点分别位于第一、三象限时，求椭圆短轴长的取值范围．

Answer 1

分析：（I）利用“点差法”和中点坐标公式、斜率计算公式即可得出；
（II）利用两条直线的夹角公式、准线方程和a²=b²+c²即可得出；
（III）设AB直线的方程为y=x+c与椭圆方程联立，可得根与系数的关系．由于A、B两点分别位于第一、三象限，可得x₁x₂＜0．得到b，c的关系．再利用准线方程和a，b，c的关系即可用b表示c，进而得到取值范围．

解答：解：（I）设A（x₁，y₁），B（x₂，y₂），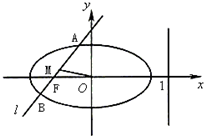
∵

x 2 1

a2

+

y 2 1

b2

=1，

x 2 2

a2

+

y 2 2

b2

=1．
两式相减，得：

y1-y2

x1-x2

•

y1+y2

x1+x2

=-

b2

a2

．
∵kAB=

y1-y2

x1-x2

=1，kOM=

y1+y2

x1+x2

．
∴kOM=-

b2

a2

．
（II）因为直线AB与OM的夹角为α，tanα=2
由（I）知k_AB=1，kOM=-

b2

a2

．
∴tanα=

1+ b2 a2

1- b2 a2

=2①
又椭圆中心在坐标原点O，一条准线的方程是x=1，
∴

a2

c

=1②
在椭圆中，a²=b²+c²③
联立①②③，解得：

a2= 2 3 b2= 2 9

所以，椭圆的方程为  

x2

2 3

+

y2

2 9

=1．
（III）设AB直线的方程为y=x+c
由

y=x+c x2 a2 + y2 b2 =1

消元得（a²+b²）x²+2a²cx+a²c²-a²b²=0
∵A、B两点分别位于第一、三象限，
∴x1x2＜0，即

c2-b2

a2+b2

＜0，∴0＜c＜b，
又

a2 c =1 a2-b2=c2

，即c2-c+b2=0．
当△=1-4b2≥0即0＜b≤

1

2

时，c=

1- 1-4b2

2

＜b
解得：0＜b＜

1

2

，0＜2b＜1．
∴椭圆短轴长的取值范围为（0，1）．

点评：熟练掌握椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立得到根与系数的关系、中点坐标公式、斜率计算公式、两条直线的夹角公式等是解题的关键．