Question

如图，在棱长为2的正方体ABCD-A₁B₁C₁D₁中，E、F分别为BD、BB₁的中点．

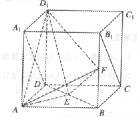(I)求证：EF∥平面A₁B₁CD；

(Ⅱ)求证：EF上AD₁；   

(Ⅲ)求三棱锥D₁-AEF的体积．

Answer 1

解：(I)连结B₁D．在△BB₁D内，E、F分别为BD、BB₁的中点，∴ EF∥B₁D．

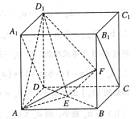又 ∵  B₁D在平面A₁B₁CD内，EF               在平面A₁B₁CD外，

    ∴ EF∥平面A₁B₁CD．   

    (Ⅱ) ∵ ABCD-A₁B₁C₁D₁是正方体，

∴ AD₁⊥A₁D，AD₁⊥A₁B₁，∴ AD₁⊥平面A₁B₁D．∴ AD₁⊥B₁D

    又由上问知道，EF∥B₁D，∴ EF⊥ AD₁．   

    (Ⅲ)由上问知，EF⊥AD₁，又显然EF⊥AE，∴ EF⊥平面AED₁．

    ∴ EF就是三棱锥F-AED₁的高．又∵AE⊥平面BB₁D₁D，∴ AE⊥D₁E

    ∴ 三棱锥F-AED₁的底面AED₁是直角三角形．  

    易求得

    ∴ 三棱锥D₁-AEF的体积