题目内容
已知函数f(x)满足:当x≥4时,f(x)= x;当x<4时,f(x)=f(x+1).则f(2+log23)=
x;当x<4时,f(x)=f(x+1).则f(2+log23)=
A. | B. | C. | D. |
A.
解析试题分析:因为 ,所以f(2+log23)=
,所以f(2+log23)= ,
,
又 ,所以
,所以 .
.
考点: 分段函数的应用.
点评:本题考查分段函数求值及指数对数的性质,对基本运算规则掌握的熟练程度要求较高.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
已知 的最小值为
的最小值为 ,若函数
,若函数 的解集为
的解集为
A. | B. | C. | D. |
对一元二次方程 的两个根的情况,判断正确的是
的两个根的情况,判断正确的是
| A.一根小于1,另一根大于3 | B.一根小于-2,另一根大于2 |
| C.两根都小于0 | D.两根都大于2 |
若 ,
, ,则
,则
A. | B. | C. | D. |
使“ ”成立的一个充分不必要条件是 ( )
”成立的一个充分不必要条件是 ( )
A.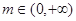 | B. |
C. | D. |
设函数 则
则 的值为 ( )
的值为 ( )
| A.a, b中较大的数 | B.a, b中较小的数 | C. a | D.b |
下列式子正确的是 ( )
A. | B. |
C. | D. |
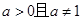 时,函数
时,函数 的图象只可能( )
的图象只可能( )
 )x的图象只可能是( )
)x的图象只可能是( )