Question

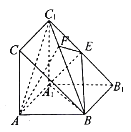
【题目】如图，四面体ABCD中，O是BD的中点，CA=CB=CD=BD=2，AB=AD=．

（1）求证：AO⊥平面BCD；

（2）求二面角O﹣AC﹣D的余弦值．

Answer 1

【答案】（1）证明略（2）

【解析】

（1）由题意，求得，利用勾股定理证得，利用线面垂直的判定定理，即可得到平面.

（2）由（1）知两两垂直，以点为原点建立空间直角坐标系，求得平面和平面的法向量为，利用向量的夹角公式，即可求解.

（1）因为四面体ABCD中，O是BD的中点，所以CA=CB=CD=BD=2，AB=AD=,

所以，

所以，所以，

因为，所以平面.

（2）由（1）知两两垂直，以点为原点建立空间直角坐标系，

则,

∴，

设平面的法向量为，

则，取，则，

又由平面的一个法向量为，

设二面角的平面角为，易知为锐角，

则，

所以二面角的余弦值为.