题目内容
若集合M={y|y=x-2}，P={y|y=
}，那么M∩P=（ ）
| x-1 |
| A、（1，+∞） |
| B、[1，+∞） |
| C、（0，+∞） |
| D、[0，+∞） |
分析：先化简这两个集合，利用两个集合的交集的定义求出M∩P．
解答：解：∵M={y|y=
}={y|y＞0}，P={y|y=
}={y|y≥0}，
∴M∩P={y|y＞0}=（0，+∞），
故选C．
| 1 |
| x2 |
| x-1 |
∴M∩P={y|y＞0}=（0，+∞），
故选C．
点评：本题考查函数的值域的求法，两个集合的交集的定义，化简这两个集合是解题的关键．
练习册系列答案
相关题目
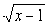}，则M∩P等于 （ ）
，则M∩P=（ ）
，则M∩P=（ ）
，则M∩P=（ ）