题目内容

已知椭圆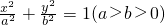 $数学公式$ 的右焦点为F，?为右准线，过F作椭圆的弦AB，以AB为直径的圆与?的关系

A.
相交
B.
相切
C.
相离
D.
不确定

C
分析：过焦点的弦为AB的中点是M且到准线的距离是d．设A到右准线的距离d₁=|PF|，B到准线的距离d₂=|QF|．结合中位线的定义与椭圆的定义可得：所做圆的半径r= $\text{[math]}$ ，而 $\text{[math]}$ （d₁+d₂）= $\text{[math]}$ = $\text{[math]}$ ，结合0＜e＜1进而得到答案．
解答：过焦点的弦为AB的中点是M且到准线的距离是d，设A到右准线的距离d₁=|PF|，B到准线的距离d₂=|QF|．
结合中位线的定义与椭圆的定义可得：所做圆的半径r= $\text{[math]}$ ，
∵ $\text{[math]}$ ，0＜e＜1
∴ $\text{[math]}$ （d₁+d₂）= $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ $\text{[math]}$ =r
由直线与圆的位置关系可知，直线与圆相离
故选C
点评：本题主要考查了直线与圆的位置关系的判定，解决此类问题的关键是熟练掌椭圆线的定义

练习册系列答案

快乐暑假假期面对面南方出版社系列答案

期末加假期期末大赢家冲刺100分西安出版社系列答案

假期作业自我检测吉林出版集团有限责任公司系列答案

暑假新时空系列答案

赢在假期衔接教材寒假合肥工业大学出版社系列答案

暑假总动员期末复习暑假衔接云南科技出版社系列答案

假日综合吉林出版集团有限责任公司系列答案

寒假学习与生活假日知新系列答案

假期快乐练培优暑假作业西安出版社系列答案

快乐假期作业延边教育出版社系列答案

相关题目

已知椭圆的右焦点为F，右准线为l，A、B是椭圆上两点，且|AF|：|BF|=3：2，直线AB与l交于点C，则B分有向线段

所成的比为（　　）

（08年黄冈中学二模理）如图，已知椭圆的右焦点为F，过F的直线（非x轴）交椭圆于M、N两点，右准线交x轴于点K，左顶点为A.

（1）求证：KF平分∠MKN；

（2）直线AM、AN分别交准线于点P、Q，设直线MN的倾斜角为，试用表示线段PQ的长度|PQ|，并求|PQ|的最小值.

（14分）已知椭圆的右焦点为F，上顶点为A，P为C上任一点，MN是圆的一条直径，若与AF平行且在y轴上的截距为的直线恰好与圆相切。

（1）已知椭圆的离心率；

（2）若的最大值为49，求椭圆C的方程。

如图，已知椭圆的右焦点为F，过F的直线（非x轴）交椭圆于M、N两点，右准线交x轴于点K，左顶点为A．

（Ⅰ）求证：KF平分∠MKN；

（Ⅱ）直线AM、AN分别交准线于点P、Q，

设直线MN的倾斜角为，试用表示

线段PQ的长度|PQ|，并求|PQ|的最小值．

（本小题满分14分）已知椭圆的右焦点为F，上顶点为A，P为C上任一点，MN是圆的一条直径，若与AF平行且在y轴上的截距为的直线恰好与圆相切．

（Ⅰ）求椭圆的离心率；

（Ⅱ）若的最大值为49，求椭圆C的方程．