Question

已知中心在原点的双曲线C的右焦点为（2，0），右顶点为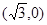

（1）求双曲线C的方程；

（2）若直线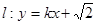与双曲线C恒有两个不同的交点A和B，且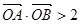（其中O为原点）. 求k的取值范围.

 

Answer 1

【答案】

（1）（2）

【解析】本试题主要是考查了双曲线方程的求解，已知直线与双曲线的位置关系的综合运用。

（1）因为中心在原点的双曲线C的右焦点为（2，0），右顶点为根据其性质可知a,b的值，得到双曲线C的方程；

（2）将 结合韦达定理和向量的关系得到参数k的关系式，利用向量的不等式得到k的范围。

解：（Ⅰ）设双曲线方程为 

由已知得

故双曲线C的方程为……….4分

（Ⅱ）将 

由直线l与双曲线交于不同的两点得

即①……………6分

设，则

而

………8分

于是

    ②……………10分

由①、②得  

故k的取值范围为…………12分