题目内容
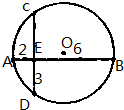在右图的圆中，弦AB、CD相交于E且互相垂直，若线段AE、EB和ED的长分别为2、6和3，则圆的直径长为| 65 |
| 65 |
分析：由相交弦定理，可求出CE的长，过O做OM⊥AB于M，ON⊥CD于N，求出EM和DN的值后，可由勾股定理得到圆的直径．
解答：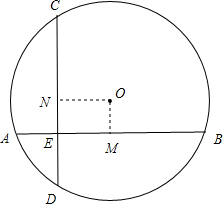
解：∵线段AE、EB和ED的长分别为2、6和3，
∴CE=
=4
过O做OM⊥AB于M，ON⊥CD于N
则EM=NO=
AB-AE=2
DN=
DC=
圆直径2OD=2
故答案为：
解：∵线段AE、EB和ED的长分别为2、6和3，∴CE=
| AE•EB |
| ED |
过O做OM⊥AB于M，ON⊥CD于N
则EM=NO=
| 1 |
| 2 |
DN=
| 1 |
| 2 |
| 7 |
| 2 |
圆直径2OD=2
| DN2+ON2 |
| 65 |
故答案为：
| 65 |
点评：本题考查的知识点相交弦定理，勾股定理，其中过O做OM⊥AB于M，ON⊥CD于N，并求出EM和DN的值，是解答的关键．
练习册系列答案
相关题目
A．选修4-1：几何证明选讲
，向量
．求向量
，使得A2
=
． 
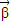（φ为参数）的右焦点，且与直线
（t为参数）平行的直线的普通方程．