题目内容
下表显示出函数值y随自变量x变化的一组数据,由此可判断它最可能的函数模型为
| x | -2 | -1 | 0 | 1 | 2 | 3 |
| y |  |  | 1 | 4 | 16 | 64 |
- A.一次函数模型
- B.二次函数模型
- C.指数函数模型
- D.对数函数模型
C
分析:由于变量可以取负数,故函数模型不可能是对数函数模型;取点(0,1),(1,4),(2,16),设出函数解析式,代入验证即可得到结论.
解答:由于变量可以取负数,故函数模型不可能是对数函数模型;
取点(0,1),(1,4),(2,16),
设一次函数y=kx+b(k≠0),则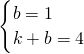 ,解得b=1,k=3,
,解得b=1,k=3,
∴y=3x+1,当x=2时,y=7,,所以不可能是一次函数模型;
设二次函数y=ax2+bx+c(a≠0),则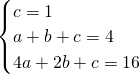 ,
,
∴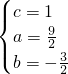 ,即y=
,即y=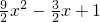
当x=-1时,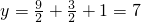 ,故不满足题意;
,故不满足题意;
设指数函数y=ax(a>0,a≠1),则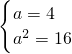 ,∴a=4,
,∴a=4,
∴指数函数y=4x,满足题意
故选C.
点评:本题考查函数模型的选择,考查学生分析解决问题的能力,属于中档题.
分析:由于变量可以取负数,故函数模型不可能是对数函数模型;取点(0,1),(1,4),(2,16),设出函数解析式,代入验证即可得到结论.
解答:由于变量可以取负数,故函数模型不可能是对数函数模型;
取点(0,1),(1,4),(2,16),
设一次函数y=kx+b(k≠0),则
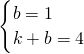 ,解得b=1,k=3,
,解得b=1,k=3,∴y=3x+1,当x=2时,y=7,,所以不可能是一次函数模型;
设二次函数y=ax2+bx+c(a≠0),则
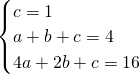 ,
,∴
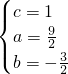 ,即y=
,即y=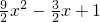
当x=-1时,
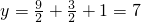 ,故不满足题意;
,故不满足题意;设指数函数y=ax(a>0,a≠1),则
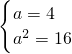 ,∴a=4,
,∴a=4,∴指数函数y=4x,满足题意
故选C.
点评:本题考查函数模型的选择,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下表显示出函数值y随自变量x变化的一组数据,由此判断它最可能的函数模型是
|
x |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Y |
15 |
17 |
19 |
21 |
23 |
25 |
27 |
A 一次函数模型 B 二次函数模型 C 指数函数模型 D 对数函数模型
下表显示出函数值y随自变量x变化的一组数据,由此判断它最可能的函数模型是
|
x |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Y |
15 |
17 |
19 |
21 |
23 |
25 |
27 |
A 一次函数模型 B 二次函数模型 C 指数函数模型 D 对数函数模型
下表显示出函数值y随自变量x变化的一组数据,由此判断它最可能的函数模型是
|
x |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Y |
15 |
17 |
19 |
21 |
23 |
25 |
27 |
A 一次函数模型 B 二次函数模型 C 指数函数模型 D 对数函数模型