题目内容
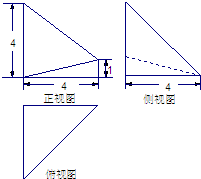 已知几何体A-BCED的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
已知几何体A-BCED的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.(1)求此几何体的体积V的大小;
(2)求异面直线DE与AB所成角的余弦值;
(3)试探究在DE上是否存在点Q,使得AQ⊥BQ并说明理由.
分析:(1)由该几何体的三视图知AC⊥面BCED,且EC=BC=AC=4,BD=1,则体积可以求得.
(2)求异面直线所成的角,一般有两种方法,一种是几何法,其基本解题思路是“异面化共面,认定再计算”,即利用平移法和补形法将两条异面直线转化到同一个三角形中,结合余弦定理来求.还有一种方法是向量法,即建立空间直角坐标系,利用向量的代数法和几何法求解.
(3)假设存在这样的点Q,使得AQ⊥BQ.
解法一:通过假设的推断、计算可知以O为圆心、以BC为直径的圆与DE相切.
解法二:在含有直线与平面垂直垂直的条件的棱柱、棱锥、棱台中,也可以建立空间直角坐标系,设定参量求解.这种解法的好处就是:1、解题过程中较少用到空间几何中判定线线、面面、线面相对位置的有关定理,因为这些可以用向量方法来解决.2、即使立体感稍差一些的学生也可以顺利解出,因为只需画个草图以建立坐标系和观察有关点的位置即可.
以C为原点,以CA,CB,CE所在直线为x,y,z轴建立空间直角坐标系.设满足题设的点Q存在,其坐标为(0,m,n),点Q在ED上,∴存在λ∈R(λ>0),使得
=λ
,解得λ=4,∴满足题设的点Q存在,其坐标为(0,
,
).
(2)求异面直线所成的角,一般有两种方法,一种是几何法,其基本解题思路是“异面化共面,认定再计算”,即利用平移法和补形法将两条异面直线转化到同一个三角形中,结合余弦定理来求.还有一种方法是向量法,即建立空间直角坐标系,利用向量的代数法和几何法求解.
(3)假设存在这样的点Q,使得AQ⊥BQ.
解法一:通过假设的推断、计算可知以O为圆心、以BC为直径的圆与DE相切.
解法二:在含有直线与平面垂直垂直的条件的棱柱、棱锥、棱台中,也可以建立空间直角坐标系,设定参量求解.这种解法的好处就是:1、解题过程中较少用到空间几何中判定线线、面面、线面相对位置的有关定理,因为这些可以用向量方法来解决.2、即使立体感稍差一些的学生也可以顺利解出,因为只需画个草图以建立坐标系和观察有关点的位置即可.
以C为原点,以CA,CB,CE所在直线为x,y,z轴建立空间直角坐标系.设满足题设的点Q存在,其坐标为(0,m,n),点Q在ED上,∴存在λ∈R(λ>0),使得
| EQ |
| QD |
| 16 |
| 5 |
| 8 |
| 5 |
解答: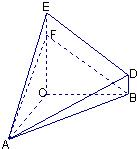 解:(1)由该几何体的三视图知AC⊥面BCED,且EC=BC=AC=4,BD=1,
解:(1)由该几何体的三视图知AC⊥面BCED,且EC=BC=AC=4,BD=1,
∴S梯形BCED=
×(4+1)×4=10
∴V=
•S梯形BCED•AC=
×10×4=
.
即该几何体的体积V为16.(3分)
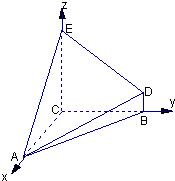
(2)解法1:过点B作BF∥ED交EC于F,连接AF,
则∠FBA或其补角即为异面直线DE与AB所成的角.(5分)
在△BAF中,
 ∵AB=4
∵AB=4
,
BF=AF=
=5.
∴cos∠ABF=
=
.
即异面直线DE与AB所成的角的余弦值为
.(7分)
解法2:以C为原点,以CA,CB,CE所在直线为x,y,z轴建立空间直角坐标系.
则A(4,0,0),B(0,4,0),D(0,4,1),E(0,0,4)
∴
=(0,-4,3),
=(-4,4,0),
∴cos<
,
>=-
∴异面直线DE与AB所成的角的余弦值为
.
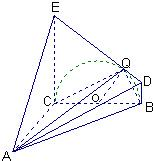 (3)解法1:在DE上存在点Q,使得AQ⊥BQ.(8分)
(3)解法1:在DE上存在点Q,使得AQ⊥BQ.(8分)
取BC中点O,过点O作OQ⊥DE于点Q,则点Q满足题设.(10分)
连接EO、OD,在Rt△ECO和Rt△OBD中
∵
=
=2
∴Rt△ECO∽Rt△OBD
∴∠EOC=∠OBD
∵∠EOC+∠CEO=90°
∴∠EOC+∠DOB=90°
∴∠EOB=90°.(11分)
∵OE=
=2
,OD=
=
∴OQ=
=
=2∴以O为圆心、以BC为直径的圆与DE相切.
切点为Q
∴BQ⊥CQ
∵AC⊥面BCED,BQ?面CEDB
∴BQ⊥AC
∴BQ⊥面ACQ(13分)
∵AQ?面ACQ
∴BQ⊥AQ.(14分)
解法2:以C为原点,以CA,CB,CE所在直线为x,y,z轴建立空间直角坐标系.
设满足题设的点Q存在,其坐标为(0,m,n),
则
=(-4,m,n),
=(0,m-4,n)
=(0,m,n-4),
=(0,4-m,1-n)
∵AQ⊥BQ∴m(m-4)+n2=0①
∵点Q在ED上,∴存在λ∈R(λ>0)
使得
=λ
∴(0,m,n-4)=λ(0,4,m,1-n)⇒m=
,n=
②
②代入①得(
)2=⇒λ2-8λ+16=0,解得λ=4
∴满足题设的点Q存在,其坐标为(0,
,
).
 解:(1)由该几何体的三视图知AC⊥面BCED,且EC=BC=AC=4,BD=1,
解:(1)由该几何体的三视图知AC⊥面BCED,且EC=BC=AC=4,BD=1,∴S梯形BCED=
| 1 |
| 2 |
∴V=
| 1 |
| 3 |
| 1 |
| 3 |
| 40 |
| 3 |
即该几何体的体积V为16.(3分)
(2)解法1:过点B作BF∥ED交EC于F,连接AF,
则∠FBA或其补角即为异面直线DE与AB所成的角.(5分)
在△BAF中,
 ∵AB=4
∵AB=4| 2 |
BF=AF=
| 16+9 |
∴cos∠ABF=
| BF2+AB2-AF2 |
| 2BF•AB |
2
| ||
| 5 |
即异面直线DE与AB所成的角的余弦值为
2
| ||
| 5 |
解法2:以C为原点,以CA,CB,CE所在直线为x,y,z轴建立空间直角坐标系.
则A(4,0,0),B(0,4,0),D(0,4,1),E(0,0,4)
∴
| DE |
| AB |
∴cos<
| DE |
| AB |
2
| ||
| 5 |
∴异面直线DE与AB所成的角的余弦值为
2
| ||
| 5 |
 (3)解法1:在DE上存在点Q,使得AQ⊥BQ.(8分)
(3)解法1:在DE上存在点Q,使得AQ⊥BQ.(8分)取BC中点O,过点O作OQ⊥DE于点Q,则点Q满足题设.(10分)
连接EO、OD,在Rt△ECO和Rt△OBD中
∵
| EC |
| CO |
| OB |
| OD |
∴Rt△ECO∽Rt△OBD
∴∠EOC=∠OBD
∵∠EOC+∠CEO=90°
∴∠EOC+∠DOB=90°
∴∠EOB=90°.(11分)
∵OE=
| CE2+CO2 |
| 5 |
| OB2+BD2 |
| 5 |
∴OQ=
| OE•OD |
| ED |
2
| ||||
| 5 |
切点为Q
∴BQ⊥CQ
∵AC⊥面BCED,BQ?面CEDB
∴BQ⊥AC
∴BQ⊥面ACQ(13分)
∵AQ?面ACQ
∴BQ⊥AQ.(14分)
解法2:以C为原点,以CA,CB,CE所在直线为x,y,z轴建立空间直角坐标系.
设满足题设的点Q存在,其坐标为(0,m,n),
则
| AQ |
| BQ |
| EQ |
| QD |
∵AQ⊥BQ∴m(m-4)+n2=0①
∵点Q在ED上,∴存在λ∈R(λ>0)
使得
| EQ |
| QD |
∴(0,m,n-4)=λ(0,4,m,1-n)⇒m=
| 4λ |
| 1+λ |
| 4+λ |
| 1+λ |
②代入①得(
| λ+4 |
| 1+λ |
∴满足题设的点Q存在,其坐标为(0,
| 16 |
| 5 |
| 8 |
| 5 |
点评:本小题主要考查空间线面关系、面面关系、二面角的度量、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
相关题目
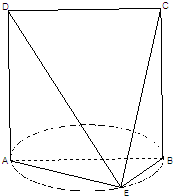 如图,已知四边形ABCD是边长为4cm的正方形,直线AD垂直于以AB为直径的圆所在的平面,点E是该圆上异于A,B的一点,连接AE、BE、DE、CE.
如图,已知四边形ABCD是边长为4cm的正方形,直线AD垂直于以AB为直径的圆所在的平面,点E是该圆上异于A,B的一点,连接AE、BE、DE、CE. 如图,已知四边形ABCD是边长为4cm的正方形,直线AD垂直于以AB为直径的圆所在的平面,点E是该圆上异于A,B的一点,连接AE、BE、DE、CE.
如图,已知四边形ABCD是边长为4cm的正方形,直线AD垂直于以AB为直径的圆所在的平面,点E是该圆上异于A,B的一点,连接AE、BE、DE、CE.