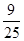题目内容
口袋中有大小、形状都相同的6个球，其中白球2个，红球4个，
（1）任取一个球投在一个面积为
的正方形内，求球落在正方形内切圆内的概率；
（2）若在袋中一次任取两个，求取到红球的概率.
（1）任取一个球投在一个面积为
的正方形内，求球落在正方形内切圆内的概率；（2）若在袋中一次任取两个，求取到红球的概率.
； （2）P (
)=
. 
（1）是典型的几何概型，如图：
（2）在袋中一次任取两个有
中方法，取到红球的的对立事件是全是白球方法有1种，所以
P(
)=
，P ()=
解：（1）圆面积为
，设“落在圆内”为事件则………………….(4分)
（2）设“取到红球”为事件则为“两个都为白球”……………6分
实验“在袋中任取两个”共有基本事件15个，……………8分
“两个都为白球”包含1个基本事件， ……………10分
所以P()=，P ()= ……………12分
（2）在袋中一次任取两个有
中方法，取到红球的的对立事件是全是白球方法有1种，所以P(
)=，P ()= 解：（1）圆面积为
，设“落在圆内”为事件则………………….(4分)（2）设“取到红球”为事件
则为“两个都为白球”……………6分实验“在袋中任取两个”共有基本事件15个，……………8分
“两个都为白球”包含1个基本事件， ……………10分
所以P(
)=，P ()= ……………12分
练习册系列答案
阅读快车系列答案
相关题目
且互相独立，灯亮的概率为 （ ）。 
