Question

已知抛物线的顶点为原点,其焦点到直线:的距离为.设为直线上的点,过点作抛物线的两条切线,其中为切点.

(Ⅰ) 求抛物线的方程；

(Ⅱ) 当点为直线上的定点时,求直线的方程；

(Ⅲ) 当点在直线上移动时,求的最小值.

Answer 1

解：(Ⅰ) 依题意,设抛物线的方程为,由结合,

解得.

   所以抛物线的方程为.  …… 4分

   (Ⅱ) 抛物线的方程为,即,求导得

设,(其中),

则切线的斜率分别为,,

所以切线的方程为,即,即

同理可得切线的方程为

因为切线均过点,所以,

所以为方程的两组解.

所以直线的方程为.  …… 8分

(Ⅲ) 由抛物线定义可知,,

所以

联立方程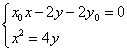,消去整理得

由一元二次方程根与系数的关系可得,

所以

又点在直线上,所以,

所以

所以当时, 取得最小值,且最小值为.  …… 13分