题目内容
已知椭圆C: ,以抛物线y2=16x的焦点为椭圆的一个焦点,且短轴一个端点与两个焦点可组成一个等边三角形,则椭圆C的离心率为( )
,以抛物线y2=16x的焦点为椭圆的一个焦点,且短轴一个端点与两个焦点可组成一个等边三角形,则椭圆C的离心率为( )A.

B.

C.

D.

【答案】分析:由题意可得椭圆C: 的焦点F2(-(4,0),则椭圆的另一个焦点F1(-4,0),短轴的一个端点B(0,b)则△BF1F2为等边三角形可得,BF1=BF2=F1F2=8,从而可得2a=16即a=8,代入椭圆的离心率公式
的焦点F2(-(4,0),则椭圆的另一个焦点F1(-4,0),短轴的一个端点B(0,b)则△BF1F2为等边三角形可得,BF1=BF2=F1F2=8,从而可得2a=16即a=8,代入椭圆的离心率公式 可求
可求
解答: 解:由题意可得,抛物线y2=16x的焦点为(4,0)即椭圆C:
解:由题意可得,抛物线y2=16x的焦点为(4,0)即椭圆C: 的焦点F2(4,0),
的焦点F2(4,0),
由题意可得,椭圆的另一个焦点F1(-4,0),短轴的一个端点B(0,b)
则由△BF1F2为等边三角形可得,BF1=BF2=F1F2=8
由椭圆的定义可得2a=16即a=8
∴ =
=
故选B
点评:本题主要考查了利用椭圆的性质求解椭圆的方程,椭圆的性质,属于基本知识的简单应用.
 的焦点F2(-(4,0),则椭圆的另一个焦点F1(-4,0),短轴的一个端点B(0,b)则△BF1F2为等边三角形可得,BF1=BF2=F1F2=8,从而可得2a=16即a=8,代入椭圆的离心率公式
的焦点F2(-(4,0),则椭圆的另一个焦点F1(-4,0),短轴的一个端点B(0,b)则△BF1F2为等边三角形可得,BF1=BF2=F1F2=8,从而可得2a=16即a=8,代入椭圆的离心率公式 可求
可求解答:
 解:由题意可得,抛物线y2=16x的焦点为(4,0)即椭圆C:
解:由题意可得,抛物线y2=16x的焦点为(4,0)即椭圆C: 的焦点F2(4,0),
的焦点F2(4,0),由题意可得,椭圆的另一个焦点F1(-4,0),短轴的一个端点B(0,b)
则由△BF1F2为等边三角形可得,BF1=BF2=F1F2=8
由椭圆的定义可得2a=16即a=8
∴
 =
=
故选B
点评:本题主要考查了利用椭圆的性质求解椭圆的方程,椭圆的性质,属于基本知识的简单应用.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 :
: ,以抛物线
,以抛物线 的焦点为椭圆的一个焦点,且短轴一个端点与两个焦点可组成一个等边三角形,则椭圆C的离心率为
的焦点为椭圆的一个焦点,且短轴一个端点与两个焦点可组成一个等边三角形,则椭圆C的离心率为  A.
A. B.
B. 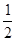 C.
C.  D.
D. 
 ,以抛物线y2=16x的焦点为椭圆的一个焦点,且短轴一个端点与两个焦点可组成一个等边三角形,则椭圆C的离心率为( )
,以抛物线y2=16x的焦点为椭圆的一个焦点,且短轴一个端点与两个焦点可组成一个等边三角形,则椭圆C的离心率为( )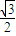



 ,以抛物线y2=16x的焦点为椭圆的一个焦点,且短轴一个端点与两个焦点可组成一个等边三角形,则椭圆C的离心率为
,以抛物线y2=16x的焦点为椭圆的一个焦点,且短轴一个端点与两个焦点可组成一个等边三角形,则椭圆C的离心率为 



 以抛物线
以抛物线 的焦点为焦点,且短轴一个端点与两个焦点可组成一个等边三角形,那么椭圆C.的离心率为 ( )
的焦点为焦点,且短轴一个端点与两个焦点可组成一个等边三角形,那么椭圆C.的离心率为 ( ) B.
B. C.
C.  D.
D.
