题目内容
Rt△ABC所在平面α外有一点P,∠C=90°,PC=24,PD⊥AC于D,PE⊥BC于E,且PD=PE=(1)P点到平面α的距离;
(2)PC和平面α所成角的大小.
解:(1)作PO⊥α于O,则PO为P点到平面α的距离,连结OC,∠PCO为PC和平面α所成的角.连结OE、OD.
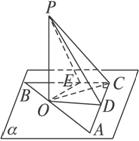
∵PD=PE,PE⊥BC于E,PD⊥AC于D,
∴PD、PE在平面α内的射影分别为OD、OE,且OE=OD,OE⊥BC,OD⊥AC,
即四边形ODCE中,OE=OD,且∠OEC=∠ODC=∠C=90°.
∴四边形ODCE为正方形,OC=![]() OE.
OE.
设OP=x,则
OC2=PC2-OP2=242-x2, ①
OE2=PE2-OP2=(![]() )2-x2, ②
)2-x2, ②
OC=![]() OE, ③
OE, ③
解①②③组成的方程组得x=12.
(2)在Rt△POC中,sin∠PCO=![]() =
=![]() ,
,
∴∠PCO=30°.
∴P点到平面α的距离为12,
PC与平面α成的角为30°.
小结:利用图形中的公共量关系构造方程并解方程,是立体几何解决问题的方法之一.

练习册系列答案
相关题目
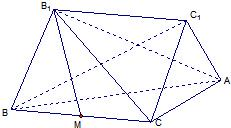 如图:已知BB1,CC1是Rt△ABC所在平面同侧的两条相等的斜线段,它们与平面ABC所成的角均为60°,且BB1∥CC1,线段BB1的端点B1在平面ABC的射影M恰是BC的中点,已知BC=2,∠ACB=90°
如图:已知BB1,CC1是Rt△ABC所在平面同侧的两条相等的斜线段,它们与平面ABC所成的角均为60°,且BB1∥CC1,线段BB1的端点B1在平面ABC的射影M恰是BC的中点,已知BC=2,∠ACB=90° (2013•温州一模)如图,已知平面QBC与直线PA均垂直于Rt△ABC所在平面,且PA=AB=AC.
(2013•温州一模)如图,已知平面QBC与直线PA均垂直于Rt△ABC所在平面,且PA=AB=AC. 如图,点P是Rt△ABC所在平面外一点,∠ABC=90°,点P在平面ABC上的射影在AB上,E、F、G分别为AB、PB、PC的中点.若PA=BC=4,求△EFG的面积.
如图,点P是Rt△ABC所在平面外一点,∠ABC=90°,点P在平面ABC上的射影在AB上,E、F、G分别为AB、PB、PC的中点.若PA=BC=4,求△EFG的面积. (2013•温州一模)如图,已知平面QBC与直线PA均垂直于Rt△ABC所在平面,且PA=AB=AC,
(2013•温州一模)如图,已知平面QBC与直线PA均垂直于Rt△ABC所在平面,且PA=AB=AC, ,两直角边分别为6、8,平面α外一点P到A,B,C三点的距离都是13,则点P 到平面
,两直角边分别为6、8,平面α外一点P到A,B,C三点的距离都是13,则点P 到平面