题目内容
 (2011•江苏二模)如图,在直三棱柱ABC-A1B1C1中,AB=AC=AA1=3a,BC=2a,D是BC的中点,E为AB的中点,F是C1C上一点,且CF=2a.
(2011•江苏二模)如图,在直三棱柱ABC-A1B1C1中,AB=AC=AA1=3a,BC=2a,D是BC的中点,E为AB的中点,F是C1C上一点,且CF=2a.(1)求证:C1E∥平面ADF;
(2)试在BB1上找一点G,使得CG⊥平面ADF;
(3)求三棱锥D-AB1F的体积.
分析:(1)连接CE交AD于O,连接FO,由
=
=
可证FO∥EC1,根据线面平行的判定定理可证
(2)在平面C1CBB1内,过C作CG⊥DF,交BB1于G,由AD⊥BC,CC1⊥AD可证AD⊥平面C1CBB1
进而可证AD⊥CG,CG⊥DF,从而可证
(3)由题意可得VD-AFB1=VA-B1FD=
S△FDB1•AD,可求
| CO |
| CE |
| CF |
| CC1 |
| 2 |
| 3 |
(2)在平面C1CBB1内,过C作CG⊥DF,交BB1于G,由AD⊥BC,CC1⊥AD可证AD⊥平面C1CBB1
进而可证AD⊥CG,CG⊥DF,从而可证
(3)由题意可得VD-AFB1=VA-B1FD=
| 1 |
| 3 |
解答:证明:(1)∵AB=AC,D为BC的中点
∵E为AB的中点,连接CE交AD于O,连接FO,
∴
=
=
∴FO∥EC1(2分)
∵FO⊆平面AFD,C1E?平面AFD(4分)
∴C1E∥平面AFD(5分)
(2)在平面C1CBB1内,过C作CG⊥DF,交BB1于G
在△RtFCD 和△RtCBG中FC=CB,∠CFD=∠BCG
∴Rt△FCD≌Rt△CBG(6分)
而AD⊥BC,CC1⊥AD且CC1∩BC=C
∴AD⊥平面C1CBB1(8分)
∵CG⊆平面C1CBB1
∴AD⊥CG,
∵CG⊥DF,AD∩FD=D
∴CG⊥平面ADF
此时BG=CD=a(10分)
(3)AD⊥BCC1B1
∴VD-AFB1=VA-B1FD=
S△FDB1•AD(12分)
=
×
B1F•FD•AD
=
a3(14分)
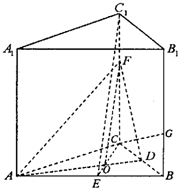
∵E为AB的中点,连接CE交AD于O,连接FO,
∴
| CO |
| CE |
| CF |
| CC1 |
| 2 |
| 3 |
∴FO∥EC1(2分)
∵FO⊆平面AFD,C1E?平面AFD(4分)
∴C1E∥平面AFD(5分)
(2)在平面C1CBB1内,过C作CG⊥DF,交BB1于G
在△RtFCD 和△RtCBG中FC=CB,∠CFD=∠BCG
∴Rt△FCD≌Rt△CBG(6分)
而AD⊥BC,CC1⊥AD且CC1∩BC=C
∴AD⊥平面C1CBB1(8分)
∵CG⊆平面C1CBB1
∴AD⊥CG,
∵CG⊥DF,AD∩FD=D
∴CG⊥平面ADF
此时BG=CD=a(10分)
(3)AD⊥BCC1B1
∴VD-AFB1=VA-B1FD=
| 1 |
| 3 |
=
| 1 |
| 3 |
| 1 |
| 2 |
=
5
| ||
| 3 |

点评:本题主要考查了直线于平面平行的判定定理、直线与平面垂直的判定定理的应用,利用等体积法求解三棱锥的体积是高考的重点题型,要注意掌握

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目

 (2011•江苏二模)在如图所示的流程图中,输出的结果是
(2011•江苏二模)在如图所示的流程图中,输出的结果是