��Ŀ����
�����������⣺�١�x=2���ǡ�x2=4���ij�ֲ���Ҫ������
����A={x||x|��3}��B={y|y=-x2+t}����A��B=∅����ʵ��t��ȡֵ��ΧΪ[3��+�ޣ���
����log2x+logx2��2����x��1��
�ܴ���x��y��R��ʹsin��x-y��=sinx-siny��
��������P���������x��R������
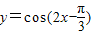 �ĵݼ�����Ϊ
�ĵݼ�����Ϊ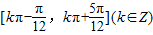 ������q������x��R��ʹtanx=1�������⡰p��q���������⣮
������q������x��R��ʹtanx=1�������⡰p��q���������⣮��������������Ϊ ��
���𰸡����������ݳ�Ҫ�����Ķ��壬�����жϢٵ���٣�
�����ֵ����ʽ���A�����ݶ��κ��������ʿ������B���������ݼ��Ͻ����Ķ��壬���жϢڵ���٣�
���ݶ������������ʼ���������ʽ�������жϢ۵���٣�
��x=y=0ʱ�����жϢܵ���٣�
�������Һ����ĵ����ԣ������жϢݵ���٣�
����⣺����x=2��ʱ����x2=4������������x2=4��ʱ����x=±2���ʡ�x=2����һ�����������١�x=2���ǡ�x2=4���ij�ֲ���Ҫ������ȷ��
A={x||x|��3}=[-3��3]��B={y|y=-x2+t}=��-�ޣ�t]����A��B=�գ���ʵ��t��ȡֵ��Χ��-�ޣ�-3�����ʢڴ���
��x��1ʱ��log2x��0��logx2��0��log2x+logx2��2 =2����0��x��1ʱ��log2x��0��logx2��0��log2x+logx2��-2
=2����0��x��1ʱ��log2x��0��logx2��0��log2x+logx2��-2 =-2��
=-2��
��log2x+logx2��2ʱ��x��1��������ȷ��
��x=y=0ʱ��sin��x-y��=sin��0��=0=sin0-sin0=0���ʢ���ȷ��
����P����2k�� ��2k��+��k��Z������x��
��2k��+�У�k��Z������x�� ���ʶ������x��R������
���ʶ������x��R������ �ĵݼ�����Ϊ
�ĵݼ�����Ϊ �Ǽ����⣬�����⡰p��q���Ǽ����⣬�ʢݴ���
�Ǽ����⣬�����⡰p��q���Ǽ����⣬�ʢݴ���
�ʴ�Ϊ���٢ۢ�
���������⿼���֪ʶ�������������жϣ���Ҫ����������ʽ�Ľⷨ�����ϵ����㣬�������������ʣ���������ʽ�����Һ����Ķ��壬�����Һ����ĵ����ԣ�����������������֪ʶ���ǽ��Ĺؼ���
�����ֵ����ʽ���A�����ݶ��κ��������ʿ������B���������ݼ��Ͻ����Ķ��壬���жϢڵ���٣�
���ݶ������������ʼ���������ʽ�������жϢ۵���٣�
��x=y=0ʱ�����жϢܵ���٣�
�������Һ����ĵ����ԣ������жϢݵ���٣�
����⣺����x=2��ʱ����x2=4������������x2=4��ʱ����x=±2���ʡ�x=2����һ�����������١�x=2���ǡ�x2=4���ij�ֲ���Ҫ������ȷ��
A={x||x|��3}=[-3��3]��B={y|y=-x2+t}=��-�ޣ�t]����A��B=�գ���ʵ��t��ȡֵ��Χ��-�ޣ�-3�����ʢڴ���
��x��1ʱ��log2x��0��logx2��0��log2x+logx2��2
 =2����0��x��1ʱ��log2x��0��logx2��0��log2x+logx2��-2
=2����0��x��1ʱ��log2x��0��logx2��0��log2x+logx2��-2 =-2��
=-2����log2x+logx2��2ʱ��x��1��������ȷ��
��x=y=0ʱ��sin��x-y��=sin��0��=0=sin0-sin0=0���ʢ���ȷ��
����P����2k��
 ��2k��+��k��Z������x��
��2k��+�У�k��Z������x�� ���ʶ������x��R������
���ʶ������x��R������ �ĵݼ�����Ϊ
�ĵݼ�����Ϊ �Ǽ����⣬�����⡰p��q���Ǽ����⣬�ʢݴ���
�Ǽ����⣬�����⡰p��q���Ǽ����⣬�ʢݴ����ʴ�Ϊ���٢ۢ�
���������⿼���֪ʶ�������������жϣ���Ҫ����������ʽ�Ľⷨ�����ϵ����㣬�������������ʣ���������ʽ�����Һ����Ķ��壬�����Һ����ĵ����ԣ�����������������֪ʶ���ǽ��Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ