题目内容
已知数列{an},其中a1=
,2an=an-1(n≥2);等差数列{bn},其中b3=2,b5=6.
(1)求数列{an}的通项公式;
(2)在数列{bn}中是否存在一项bm(m为正整数),使得 b3,b5,bm成等比数列,若存在,求m的值;若不存在,说明理由.
| 1 |
| 2 |
(1)求数列{an}的通项公式;
(2)在数列{bn}中是否存在一项bm(m为正整数),使得 b3,b5,bm成等比数列,若存在,求m的值;若不存在,说明理由.
考点:等比数列的性质,数列递推式
专题:计算题,等差数列与等比数列
分析:(1)由2an=an-1,可得
=
,利用等比数列的通项公式求数列{an}的通项公式;
(2)确定数列{bn}的通项,利用b3,b5,bm成等比数列,求m的值.
| an |
| an-1 |
| 1 |
| 2 |
(2)确定数列{bn}的通项,利用b3,b5,bm成等比数列,求m的值.
解答:
解:(1)∵2an=an-1,∴
=
…(3分)
∵a1=
,∴an=
(
)n-1=
…(6分)
(2)∵等差数列{bn},b3=2,b5=6,∴bn=2n-4…(9分)
∴bm=2m-4
又∵b3,b5,bm成等比数列
∴b52=b3•bm…(12分)
∴m=11…(14分)
| an |
| an-1 |
| 1 |
| 2 |
∵a1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2n |
(2)∵等差数列{bn},b3=2,b5=6,∴bn=2n-4…(9分)
∴bm=2m-4
又∵b3,b5,bm成等比数列
∴b52=b3•bm…(12分)
∴m=11…(14分)
点评:本题考查等差数列、等比数列的通项公式,考查学生的计算能力,比较基础.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
设a>0,b>0且a+b=1则
+
的最小值是( )
| 1 |
| a |
| 2 |
| b |
| A、2 | ||
| B、4 | ||
C、3+2
| ||
| D、6 |
“x=-2”是“x≠0”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
设x≥0,则 x+
的最小值是( )
| 2 |
| x+1 |
| A、2 | ||
| B、3 | ||
C、2
| ||
D、2
|
| 1 |
| 2 |
| A、2+2i | B、2-2i |
| C、i | D、-i |
tan
π的值为( )
| 16 |
| 3 |
A、-
| ||||
B、
| ||||
C、
|
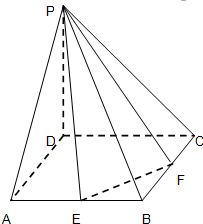 已知正方形ABCD,边长为1,过D作PD⊥平面ABCD,且PD=2,E,F分别是AB和BC的中点.
已知正方形ABCD,边长为1,过D作PD⊥平面ABCD,且PD=2,E,F分别是AB和BC的中点.