题目内容
f（x）是一次函数且2f（1）＋3f（2）＝3，2f（－1）－f（0）＝－1，则f（x）等于
A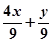． | B．36x－9 | C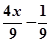． | D．9－36x |
C
解析试题分析：设f(x)=ax+b，∵2f（1）＋3f（2）＝3，2f（－1）－f（0）＝－1，∴8a+5b=3,2a-b=1，解得a=
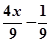，∴f（x）=，故选C
考点：本题考查了函数解析式的求法
点评：当函数的特征已知时，常常用待定系数法求解函数的解析式，属基础题
练习册系列答案
相关题目
函数
的零点所在的大致区间是（ ）
| A．（1，2） | B．（e，3） | C．（2，e） | D．(e, + ) |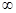
函数f(x)=2x－x3的零点所在的一个区间 ( )
| A．(0,1) | B．(1,2) | C．(2,3) | D．(3,4) |
函数f(x)=2x－x3的零点所在的一个区间是 ( )
| A．(0,1) | B．(1,2) | C．(2,3) | D．(3,4) |
函数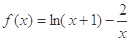
的零点所在的大致区间是（ ）
A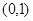． | B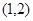． | C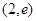． | D． |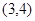
设f(x)是定义在R上的奇函数，且f(2)=0,当x>0时，有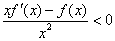
恒成立，则不等式
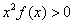的解集是
| A．(-2,0) ∪(2,+∞) | B．(-2,0) ∪(0,2) |
| C．(-∞,-2)∪(2,+∞) | D．(-∞,-2)∪(0,2) |
函数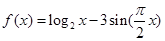
零点的个数是 （ ）
| A．5 | B．4 | C．3 | D．2 |
使得函数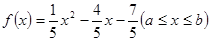
的值域为
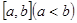的实数对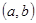
有( )对
| A．1 | B．2 | C．3 | D．无数 |