题目内容
已知O为坐标原点，点A（x，y）与点B关于x轴对称，
，则满足不等式
的点A的集合用阴影表示
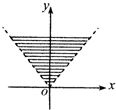
- A.
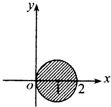
- B.
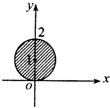
- C.
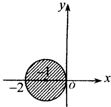
- D.
C
分析：先求出点B的坐标，并用点A的坐标表示出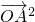
+
，最后把原不等式转化为x2+（y-1）2≤1，找出点所在的位置即可求出结论．
解答：由题得：B（-x，y），
=（0，2y）．
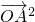∴+=x2+y2+2y=x2+（y-1）2-1．
∴不等式转化为x2+（y-1）2≤1．
故满足要求的点在以（o，1）为圆心，1为半径的圆上以及圆的内部．
故选C．
点评：本题主要考查向量的基本运算以及计算能力和转化思想的应用，属于基础题．
分析：先求出点B的坐标，并用点A的坐标表示出
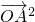+，最后把原不等式转化为x2+（y-1）2≤1，找出点所在的位置即可求出结论．解答：由题得：B（-x，y），
=（0，2y）．∴
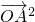+=x2+y2+2y=x2+（y-1）2-1．∴不等式
转化为x2+（y-1）2≤1．故满足要求的点在以（o，1）为圆心，1为半径的圆上以及圆的内部．
故选C．
点评：本题主要考查向量的基本运算以及计算能力和转化思想的应用，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
