题目内容
在四边形ABCD中，若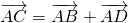
，
，则四边形ABCD是
- A.平行四边行
- B.矩形
- C.正方形
- D.菱形
D
分析：根据合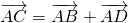以及向量加法的平行四边形法则，即可得四边形ABCD为平行四边形；再结合|
+
|=|-|可得平行四边形的对角线AC⊥BD，从而可得四边形ABCD为菱形．
解答：∵在四边形ABCD中，，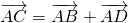
∴由向量加法加法的平行四边形法则知，线段AC是以AB、AD为邻边的平行四边形的对角线，
∴四边形ABCD是平行四边形，
再|+|=|-|两边平方可得：•=0?AC⊥BD．
即对角线互相垂直；
∴该四边形ABCD为菱形．
故选 D．
点评：利用向量的知识进行判断是解决本题的关键，本题主要考查了由向量相等及向量垂直的知识进行判断四边形的知识．
分析：根据合
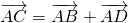以及向量加法的平行四边形法则，即可得四边形ABCD为平行四边形；再结合|+|=|-|可得平行四边形的对角线AC⊥BD，从而可得四边形ABCD为菱形．解答：∵在四边形ABCD中，
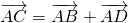，∴由向量加法加法的平行四边形法则知，线段AC是以AB、AD为邻边的平行四边形的对角线，
∴四边形ABCD是平行四边形，
再|
+|=|-|两边平方可得：•=0?AC⊥BD．即对角线互相垂直；
∴该四边形ABCD为菱形．
故选 D．
点评：利用向量的知识进行判断是解决本题的关键，本题主要考查了由向量相等及向量垂直的知识进行判断四边形的知识．
练习册系列答案
全能练考卷系列答案
一课一练课时达标系列答案
相关题目
如图所示，在四边形ABCD中，EF∥BC，FG∥AD，则