题目内容
已知函数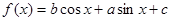 .
.
(1)当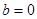 时,求
时,求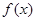 的值域;
的值域;
(2)当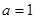 ,
,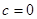 时,函数
时,函数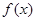 的图象关于
的图象关于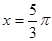 对称,求函数
对称,求函数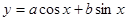 的对称轴;
的对称轴;
(3)若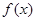 图象上有一个最低点
图象上有一个最低点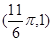 ,如果图象上每点纵坐标不变,横坐标缩短到原来的
,如果图象上每点纵坐标不变,横坐标缩短到原来的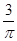 倍,然后向左平移1个单位可得
倍,然后向左平移1个单位可得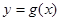 的图象,又知
的图象,又知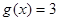 的所有正根从小到大依次为
的所有正根从小到大依次为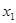 ,
,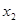 ,…
,…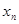 ,…且
,…且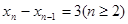 ,求
,求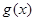 的解析式.
的解析式.
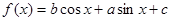 .
.(1)当
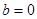 时,求
时,求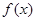 的值域;
的值域;(2)当
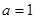 ,
,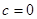 时,函数
时,函数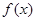 的图象关于
的图象关于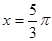 对称,求函数
对称,求函数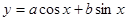 的对称轴;
的对称轴;(3)若
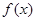 图象上有一个最低点
图象上有一个最低点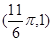 ,如果图象上每点纵坐标不变,横坐标缩短到原来的
,如果图象上每点纵坐标不变,横坐标缩短到原来的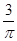 倍,然后向左平移1个单位可得
倍,然后向左平移1个单位可得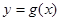 的图象,又知
的图象,又知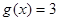 的所有正根从小到大依次为
的所有正根从小到大依次为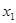 ,
,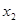 ,…
,…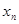 ,…且
,…且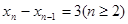 ,求
,求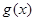 的解析式.
的解析式.(1)①当 时,值域为:
时,值域为: ; ② 当
; ② 当 时,值域为:
时,值域为: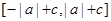 ;(2)
;(2) ;(3)
;(3)
 时,值域为:
时,值域为: ; ② 当
; ② 当 时,值域为:
时,值域为: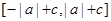 ;(2)
;(2) ;(3)
;(3)
试题分析:(1)利用正弦函数的值域和不等式性质即可求出
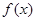 的值域,主要要分
的值域,主要要分 与
与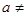 0两种情况;(2)先由对称轴过最值点列出关于
0两种情况;(2)先由对称轴过最值点列出关于 的方程,求出
的方程,求出 ,然后将函数
,然后将函数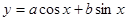 利用设辅助角公式化为一个角的三角函数,再利用求对称轴的方法求出对称轴;(3)先由设辅助角公式将函数
利用设辅助角公式化为一个角的三角函数,再利用求对称轴的方法求出对称轴;(3)先由设辅助角公式将函数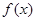 化成一个角的三角函数,利用
化成一个角的三角函数,利用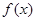 过最低点
过最低点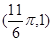 ,求出辅助角并将
,求出辅助角并将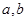 用
用 表示出来,即求出
表示出来,即求出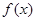 的解析式,再根据题中的图像变换求出
的解析式,再根据题中的图像变换求出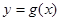 的解析式,再根据题中已知条件
的解析式,再根据题中已知条件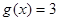 的所有正根从小到大依次为
的所有正根从小到大依次为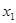 ,
,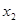 ,…
,…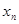 ,…且
,…且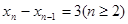 确定参数
确定参数 ,即可得到
,即可得到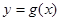 的解析式.
的解析式.试题解析:(1)当
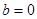 时,
时,
①当
 时,值域为:
时,值域为: ② 当
② 当 时,值域为:
时,值域为: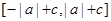
(2)当
 ,
, 时,
时, 且图象关于
且图象关于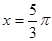 对称。
对称。∴


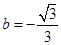 ∴函数
∴函数 即:
即: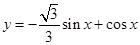 ∴
∴ 由
由
∴函数的对称轴为:

(3)由

(其中
 ,
, )
)由
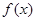 图象上有一个最低点
图象上有一个最低点 ,所以
,所以
∴
 ∴
∴
又图象上每点纵坐标不变,横坐标缩短到原来的
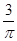 倍,然后向左平移1个单位可得
倍,然后向左平移1个单位可得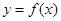 的图象,则
的图象,则
又∵
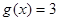 的所有正根从小到大依次为
的所有正根从小到大依次为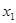 ,
,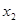 ,…
,…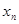 ,…,且
,…,且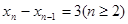
所以
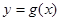 与直线
与直线 的相邻交点间的距离相等,根据三角函数的图象与性质可得以下情况:
的相邻交点间的距离相等,根据三角函数的图象与性质可得以下情况:(1)直线
 要么过
要么过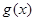 的最高点或最低点.
的最高点或最低点.即
 或
或 (矛盾),
(矛盾),

当
 时,函数的
时,函数的 ,
, 
直线
 和
和 相交,且
相交,且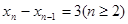 ,周期为3(矛盾)
,周期为3(矛盾)(2)
 经过
经过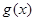 的对称中心
的对称中心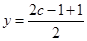
即
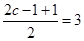 ,
,

当
 时,函数
时,函数

直线
 和
和 相交,且
相交,且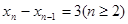 ,周期为6(满足)
,周期为6(满足)综上:
 .
.考点:三角函数图像与性质;图像变换;逻辑推理能力

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在一个周期内,当
在一个周期内,当 时,
时, 取得最小值
取得最小值 ;当
;当 时,
时,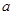 使方程
使方程 在闭区间
在闭区间 上恰有三个解
上恰有三个解 ,则
,则 ____________.
____________.  <j<
<j< ,
, 时,求f(x)的取值范围.
时,求f(x)的取值范围.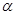 ,使
,使
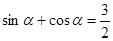
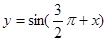 是偶函数
是偶函数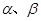 是第一象限的角,且
是第一象限的角,且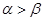 ,则
,则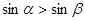 .其中正确命题的序号是________________.
.其中正确命题的序号是________________. 的图象向右平移m个单位(m>0)后,所得到的图象关于
的图象向右平移m个单位(m>0)后,所得到的图象关于 轴对称,则m的最小值是( )
轴对称,则m的最小值是( )
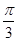


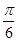 )|对一切x∈R恒成立,且f(
)|对一切x∈R恒成立,且f(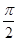 )>0,则f(x)的单调递增区间是( )
)>0,则f(x)的单调递增区间是( ) ,kπ+
,kπ+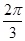 ](k∈Z)
](k∈Z) 的部分图象如图所示,则函数表达式为( ).
的部分图象如图所示,则函数表达式为( ).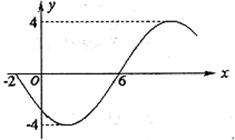
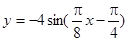



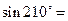 ( )
( )


