题目内容
已知函数f（x）=b•ax（其中a，b为常量且a＞0，a≠1）的图象经过点A（1，6），B（3，24），
（1）试确定f（x）；
（2）若不等式（
） x+（
） x-m≤0在x∈[0，+∞）上恒成立，求实数m的取值范围．
解：（1）∵函数f（x）=b•ax（其中a，b为常量且a＞0，a≠1）的图象经过点A（1，6），B（3，24），
∴
，解得 a=2，b=3，故f（x）=3×2x．
（2）不等式（） x+（） x-m≤0 在[0，+∞）上恒成立，故m≥
+
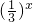在[0，+∞）上恒成立．
令g（x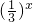）=+，则g（x）在[0，+∞）上是减函数，故m≥gmax（x）=g（0）=2，
故m的取值范围为[2，+∞）．
分析：（1）把点A（1，6），B（3，24）代入函数的解析式求出a、b的值，即可求得f（x）的解析式．
（2）由题意可得m≥+ 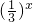在[0，+∞）上恒成立，根据 + 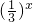在[0，+∞）上是减函数，求出它的最大值，即可求得实数m的取值范围．
点评：本题主要考查指数函数的图象和性质，函数的恒成立问题，属于中档题．
∴
，解得 a=2，b=3，故f（x）=3×2x．（2）不等式（
） x+（） x-m≤0 在[0，+∞）上恒成立，故m≥+ 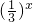在[0，+∞）上恒成立．令g（x）=
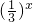+，则g（x）在[0，+∞）上是减函数，故m≥gmax（x）=g（0）=2，故m的取值范围为[2，+∞）．
分析：（1）把点A（1，6），B（3，24）代入函数的解析式求出a、b的值，即可求得f（x）的解析式．
（2）由题意可得m≥
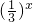+ 在[0，+∞）上恒成立，根据 + 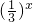在[0，+∞）上是减函数，求出它的最大值，即可求得实数m的取值范围．点评：本题主要考查指数函数的图象和性质，函数的恒成立问题，属于中档题．
练习册系列答案
相关题目