题目内容
一个多面体的三视图分别是正方形、等腰三角形和矩形，其尺寸如图，则该多面体的体积为 （ ）
| A．48cm3 | B．24cm3 |
| C．32cm3 | D．28cm3 |
A
解析
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
某三棱锥的三视图如图所示,该三棱锥的表面积是（ ）
A． | B． |
C． | D． |
六棱柱的底面是边长为3的正六边形,侧面是矩形,侧棱长为4,则其侧面积等于
| A．12 | B．48 | C．64 | D．72 |
一个与球心距离为1的平面截球体所得的圆面面积为
，则球的体积为( )
| A． 8 | B． | C． | D． |
已知三棱锥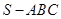
中，底面
为边长等于2的等边三角形，
垂直于底面，=1，那么直线
与平面
所成角的正弦值为
A． | B． | C． | D． |
下列几何体(如下列图)各自的三视图中，有且仅有两个视图相同的是( )
| A．①② | B．①③ | C．①④ | D．②④ |
