题目内容
设0≤θ<2π时,已知两个向量 ,则
,则 的最大值为________.
的最大值为________.
3
分析:根据题意,可得向量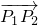 关于θ的坐标形式,再化简得到|
关于θ的坐标形式,再化简得到|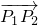 |2=10-8cosθ,结合cosθ∈[-1,1]可得当θ=π时,|
|2=10-8cosθ,结合cosθ∈[-1,1]可得当θ=π时,|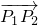 |2的最大值为18,从而得到
|2的最大值为18,从而得到 的最大值为
的最大值为 =3
=3 .
.
解答:∵
∴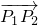 =(2+sinθ-cosθ,2-cosθ-cosθ)
=(2+sinθ-cosθ,2-cosθ-cosθ)
因此,|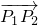 |2=(2+sinθ-cosθ)2+(2-cosθ-cosθ)2
|2=(2+sinθ-cosθ)2+(2-cosθ-cosθ)2
=4+4(sinθ-cosθ)+(sinθ-cosθ)2+4-4(sinθ+cosθ)+(sinθ+cosθ)2
=10-8cosθ
∵cosθ∈[-1,1],
∴当cosθ=-1时,|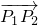 |2的最大值为18,此时θ=π
|2的最大值为18,此时θ=π
因此,可得当θ=π时, 的最大值为
的最大值为 =3
=3
故答案为:3
点评:本题给出向量 关于θ的坐标形式,求
关于θ的坐标形式,求 的最大值,着重考查了三角恒等变换、三角函数的最值和向量数量积的运算性质等知识,属于基础题.
的最大值,着重考查了三角恒等变换、三角函数的最值和向量数量积的运算性质等知识,属于基础题.

分析:根据题意,可得向量
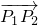 关于θ的坐标形式,再化简得到|
关于θ的坐标形式,再化简得到|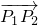 |2=10-8cosθ,结合cosθ∈[-1,1]可得当θ=π时,|
|2=10-8cosθ,结合cosθ∈[-1,1]可得当θ=π时,|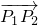 |2的最大值为18,从而得到
|2的最大值为18,从而得到 的最大值为
的最大值为 =3
=3 .
.解答:∵

∴
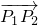 =(2+sinθ-cosθ,2-cosθ-cosθ)
=(2+sinθ-cosθ,2-cosθ-cosθ)因此,|
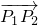 |2=(2+sinθ-cosθ)2+(2-cosθ-cosθ)2
|2=(2+sinθ-cosθ)2+(2-cosθ-cosθ)2=4+4(sinθ-cosθ)+(sinθ-cosθ)2+4-4(sinθ+cosθ)+(sinθ+cosθ)2
=10-8cosθ
∵cosθ∈[-1,1],
∴当cosθ=-1时,|
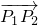 |2的最大值为18,此时θ=π
|2的最大值为18,此时θ=π因此,可得当θ=π时,
 的最大值为
的最大值为 =3
=3
故答案为:3

点评:本题给出向量
 关于θ的坐标形式,求
关于θ的坐标形式,求 的最大值,着重考查了三角恒等变换、三角函数的最值和向量数量积的运算性质等知识,属于基础题.
的最大值,着重考查了三角恒等变换、三角函数的最值和向量数量积的运算性质等知识,属于基础题. 
练习册系列答案
相关题目