题目内容
函数y=x2（x-3）的减区间是
- A.（-∞，0）
- B.（2，+∞）
- C.（0，2）
- D.（-2，2）
C
分析：求出y′，要求函数的减函数，即要y′小于0列出关于x的不等式，求出不等式的解集即可得到函数的减区间．
解答：y′=3x2-6x，由y′＜0，即3x2-6x＜0，
因式分解得3x（x-2）＜0，可化为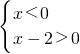
或
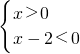
解得0＜x＜2．
故选C
点评：此题考查学生会利用导函数的正负判断函数的增减性，会求一元二次不等式的解集，是一道中档题．
分析：求出y′，要求函数的减函数，即要y′小于0列出关于x的不等式，求出不等式的解集即可得到函数的减区间．
解答：y′=3x2-6x，由y′＜0，即3x2-6x＜0，
因式分解得3x（x-2）＜0，可化为
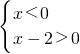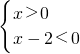
或解得0＜x＜2．
故选C
点评：此题考查学生会利用导函数的正负判断函数的增减性，会求一元二次不等式的解集，是一道中档题．
练习册系列答案
全能测控一本好卷系列答案
相关题目
函数y=x2（x-3）的减区间是（ ）
| A、（-∞，0） | B、（2，+∞） | C、（0，2） | D、（-2，2） |