题目内容
(本小题满分12分)已知函数 ,且
,且
(1)判断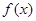 的奇偶性,并证明;
的奇偶性,并证明;
(2)判断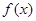 在
在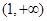 上的单调性,并证明;
上的单调性,并证明;

(3)若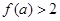 ,求
,求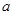 的取值范围。
的取值范围。
【答案】
(1)  为奇函数,见解析;(2)
为奇函数,见解析;(2) 在
在 上的单调递增,证明:见解析;
上的单调递增,证明:见解析;
(3) 。
。
【解析】本试题主要是考查了函数奇偶性和函数的单调性的综合运用。
(1) ,且
,且
∴  ,解得
,解得  ,根据奇偶性的定义得到奇函数的证明。
,根据奇偶性的定义得到奇函数的证明。
(2) ∵  ,由(2)知
,由(2)知 在
在 上的单调递增
上的单调递增
又 ,即
,即 ,所以可知
,所以可知
又由 的对称性可知
的对称性可知  时,
时, 同样成立,命题得证。
同样成立,命题得证。
解 ∵  ,且
,且
∴  ,解得
,解得  …………………1分
…………………1分
(1)  为奇函数,…………………………………..2分
为奇函数,…………………………………..2分
证:∵  ,定义域为
,定义域为 ,关于原点对称………………..3分
,关于原点对称………………..3分
又
所以 为奇函数………………………………4分
为奇函数………………………………4分
(2) 在
在 上的单调递增………………………………..5分
上的单调递增………………………………..5分
证明:设 ,
,
则 ……………………7分
……………………7分
∵
∴
 ,
,

故
 ,即
,即 ,
, 在
在 上的单调递增 …………9分
上的单调递增 …………9分
(3)解法一
若  ,即
,即 ,显然
,显然 ,
,
化简得 ,解得
,解得 ………………………..12分
………………………..12分
解法二、∵  ,由(2)知
,由(2)知 在
在 上的单调递增
上的单调递增
又 ,即
,即 ,所以可知
,所以可知
又由 的对称性可知
的对称性可知  时,
时, 同样成立
∴
同样成立
∴ 

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目