题目内容
以下四个命题中:
①为了了解800名学生对学校某项教改试验的意见,打算从中抽取一个容量为40的样本,考虑用系统抽样,则分段的间隔k为40.
②线性回归直线方程
=
x+
恒过样本中心(
,
),且至少过一个样本点;
③在某项测量中,测量结果ξ服从正态分布N(2,σ2)(σ>0).若ξ在(-∞,1)内取值的概率为0.1,则ξ在(2,3)内取值的概率为0.4;
其中真命题的个数为( )
①为了了解800名学生对学校某项教改试验的意见,打算从中抽取一个容量为40的样本,考虑用系统抽样,则分段的间隔k为40.
②线性回归直线方程
 |
| y |
 |
| b |
 |
| a |
. |
| x |
. |
| y |
③在某项测量中,测量结果ξ服从正态分布N(2,σ2)(σ>0).若ξ在(-∞,1)内取值的概率为0.1,则ξ在(2,3)内取值的概率为0.4;
其中真命题的个数为( )
| A、0 | B、1 | C、2 | D、3 |
分析:①系统抽样时将整个的编号分段要确定分段的间隔,当总体个数除以样本容量是整数时,则间隔确定,当不是整数时,通过从总体中删除一些个体(用简单随机抽样的方法)使剩下的总体中个体的个数能被样本容量整除;
②根据样本点中心(
,
)点必在回归直线上,不一定过样本点,即可分析真假;
③根据ξ服从正态分布N(2,σ2)(σ>0),则正态分布图象的对称轴为x=2,
根据在(-∞,1)内取值的概率为0.1,进而得到随机变量ξ在(2,3)内取值的概率.
②根据样本点中心(
. |
| x |
. |
| y |
③根据ξ服从正态分布N(2,σ2)(σ>0),则正态分布图象的对称轴为x=2,
根据在(-∞,1)内取值的概率为0.1,进而得到随机变量ξ在(2,3)内取值的概率.
解答:解:①由题意知本题是一个系统抽样,
总体中个体数是800,样本容量是40,根据系统抽样的步骤,得到分段的间隔K=
=20,故①是假命题;
②线性回归直线方程
=
x+
恒过样本中心(
,
),但不一定过样本点,故②是假命题;
③由于ξ服从正态分布N(2,σ2)(σ>0),则正态分布图象的对称轴为x=2,
故ξ在(-∞,2)内取值的概率为0.5,
又由ξ在(-∞,1)内取值的概率为0.1,则ξ在(1,2)内取值的概率为0.4
故ξ在(2,3)内取值的概率为0.4,故③是真命题;
故选:B
总体中个体数是800,样本容量是40,根据系统抽样的步骤,得到分段的间隔K=
| 800 |
| 40 |
②线性回归直线方程
 |
| y |
 |
| b |
 |
| a |
. |
| x |
. |
| y |
③由于ξ服从正态分布N(2,σ2)(σ>0),则正态分布图象的对称轴为x=2,
故ξ在(-∞,2)内取值的概率为0.5,
又由ξ在(-∞,1)内取值的概率为0.1,则ξ在(1,2)内取值的概率为0.4
故ξ在(2,3)内取值的概率为0.4,故③是真命题;
故选:B
点评:本题考查系统抽样、回归直线以及正态分布曲线的特点及曲线所表示的意义,解决本题的关键是掌握相关概念,属于基础题.

练习册系列答案
相关题目
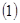 设
设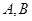 为两个定点,
为两个定点,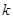 为非零常数。
为非零常数。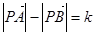 ,则动点的轨迹方程为双曲线。
,则动点的轨迹方程为双曲线。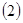 过定圆
过定圆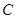 上一定点
上一定点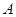 作圆的动点弦
作圆的动点弦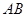 ,
,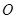 为坐标原点,若
为坐标原点,若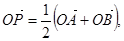 则动点
则动点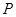 的轨迹为椭圆。
的轨迹为椭圆。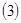 方程
方程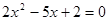 的两根可分别作为椭圆与双曲线的离心率。
的两根可分别作为椭圆与双曲线的离心率。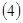 双曲线
双曲线 与椭圆
与椭圆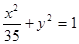 有共同的焦点。
有共同的焦点。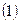 设
设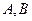 为两个定点,
为两个定点,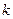 为非零常数。
为非零常数。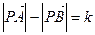 ,则动点的轨迹方程为双曲线。
,则动点的轨迹方程为双曲线。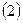 过定圆
过定圆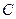 上一定点
上一定点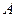 作圆的动点弦
作圆的动点弦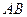 ,
,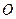 为坐标原点,若
为坐标原点,若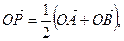 则动点
则动点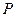 的轨迹为椭圆。
的轨迹为椭圆。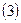 方程
方程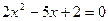 的两根可分别作为椭圆与双曲线的离心率。
的两根可分别作为椭圆与双曲线的离心率。 双曲线
双曲线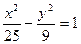 与椭圆
与椭圆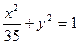 有共同的焦点。
有共同的焦点。