题目内容
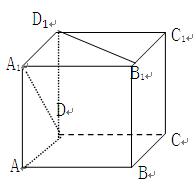
正方体ABCD- 中,求直线
中,求直线 与平面
与平面 所成的角。
所成的角。
 中,求直线
中,求直线 与平面
与平面 所成的角。
所成的角。
本试题主要考查了线面较的求解问题,能利用线面角的定义,作出角借助于直角三角形求解。
解:连接 与
与 ,交于点O,BC
,交于点O,BC  面
面  ,,BC
,,BC 
 ,正方形中,
,正方形中, ,所以
,所以 平面
平面 于点O,
于点O, 为所求角。经计算,等于
为所求角。经计算,等于 。
。
考核线面所成角的概念,线面垂直的判定。
解:连接
 与
与 ,交于点O,BC
,交于点O,BC  面
面  ,,BC
,,BC 
 ,正方形中,
,正方形中, ,所以
,所以 平面
平面 于点O,
于点O, 为所求角。经计算,等于
为所求角。经计算,等于 。
。 考核线面所成角的概念,线面垂直的判定。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
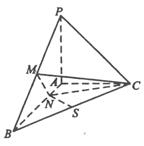
 中,
中, 是
是 中点,
中点, 是
是 的中点,则直线
的中点,则直线 与
与 所成角的大小为_______.
所成角的大小为_______.





 中,如图E、F分别是
中,如图E、F分别是  ,CD的中点,
,CD的中点, 平面ADE;
平面ADE; .
. 
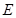 ,
,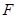 分别是正方形
分别是正方形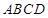 边
边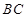 、
、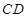 的中点,
的中点,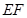 与
与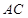 交于点
交于点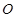 ,
,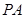 、
、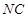 都垂直于平面
都垂直于平面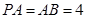 ,
, 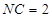 ,
,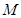 是线段
是线段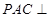 平面
平面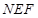 ;
;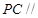 平面
平面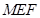 ,试求
,试求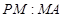 的值;
的值;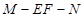 的余弦值.
的余弦值. 与AC的夹角_________.
与AC的夹角_________.
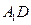 与直线
与直线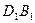 所成的角为 ▲ .
所成的角为 ▲ .