题目内容
（2013•淄博二模）函数f（x）=2x-tanx在(-
，
)上的图象大致为（ ）
| π |
| 2 |
| π |
| 2 |
分析：由题意判断函数的奇偶性以及函数在x大于0时的单调性即可推出正确结果．
解答：解：因为函数f（x）=2x-tanx在(-
，
)上满足f（-x）=-f（x），所以函数是奇函数，
故A，B不正确；
又x=
→0+，函数f（x）=2×
-tan
=
-
＞0，
故C正确，D不正确．
故选C．
| π |
| 2 |
| π |
| 2 |
故A，B不正确；
又x=
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| ||
| 3 |
故C正确，D不正确．
故选C．
点评：本题考查函数的奇偶性与函数的单调性的应用，特值法是解答选择题的好方法．
练习册系列答案
阅读快车系列答案
相关题目
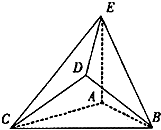（2013•淄博二模）在如图所示的几何体中，△ABC是边长为2的正三角形，AE=1，AE⊥平面ABC，平面BCD⊥平面ABC，BD=CD，且BD⊥CD．
（2013•淄博二模）如图，平行四边形ABCD中，AB=2，AD=1，∠A=60°，点M在AB边上，且AM=